
こんにちは、habrozhiteli! この本は、Tim RafgardenがCourseraとStanford Lagunitaをリードするオンラインアルゴリズムコースに基づいており、これらのコースは、彼が長年スタンフォード大学で行ってきた学生向けの講義を通して生まれました。
アルゴリズムは、コンピューターサイエンスの核心です。 ネットワークルーティングやゲノミクス計算から暗号化や機械学習まで、それらなしではできません。 「完璧なアルゴリズム」は、IT企業を雇用する際に、人生とインタビューの両方でタスクを設定し、それらを巧みに解決する真のプロになります。 Tim Rafgardenが、漸近分析、big-O表記法、アルゴリズムの分割と征服、ランダム化、ソートと選択について説明します。 この本は、すでにプログラミングの経験がある人を対象としています。 新しいレベルに移動して、全体像を確認し、低レベルの概念と数学的ニュアンスを理解します。
* 6.3。 DSelectアルゴリズム
RSelectアルゴリズムは、各入力に対して線形時間で実行されます。数学的な期待は、アルゴリズムによって実行されるランダムな選択に関連付けられます。 線形選択にはランダム化が必要ですか? このセクション以降では、この問題は、選択問題の決定論的線形アルゴリズムを使用して解決されます。
並べ替えタスクの場合、O(n log n)ランダム化QuickSortアルゴリズムの平均実行時間は決定論的なMergeSortアルゴリズムと同じであり、QuickSortとMergeSortの両方のアルゴリズムが実用に役立つアルゴリズムです。 一方、このセクションで説明する決定論的線形選択アルゴリズムは実際にはうまく機能しますが、RSelectアルゴリズムと競合しません。 これは2つの理由で発生します。DSelectアルゴリズムの時間の大きな一定の要因と、追加のRAMの割り当てと管理に関連するアルゴリズムによって実行される作業のためです。 それにもかかわらず、アルゴリズムのアイデアは非常にクールであるため、私はそれらについてあなたに話すのを助けることができません。
6.3.1。 素晴らしいアイデア:中央値の中央値
RSelectアルゴリズムは高速です。これは、ランダムなサポート要素がかなり良好である可能性が高く、分離後の入力配列のほぼバランスの取れた分割を提供し、さらに、かなり良いサポート要素が急速に進歩するためです。 ランダム化の使用が許可されていない場合、あまり多くの作業を行わずに、どのようにしてかなり良い参照要素を計算できますか?
決定論的な線形選択の独創的なアイデアは、「中央値の中央値」を真の中央値のプロキシとして使用することです。 アルゴリズムは、入力配列の要素をスポーツチームと見なし、2ラウンドでノックアウトトーナメントを開催します。そのチャンピオンはサポート要素です。 図も参照してください。 6.1。
最初のラウンドは、最初のグループとして入力配列の位置1〜5にある要素、2番目のグループとして位置6〜10にある要素などのグループステージです。 5つの要素のグループの最初のラウンドの勝者は、要素の中央値(つまり、3番目に小さい要素)として定義されます。 があるので
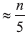
5つの要素のグループ、
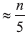
最初の勝者。 (いつものように、簡単にするために分数は無視します。)トーナメントチャンピオンは、第1ラウンドの勝者の中央値として定義されます。
6.3.2。 DSelectアルゴリズムの擬似コード
中央値の中央値を実際に計算する方法は? 中央値の各計算には5つの要素しか含まれていないため、消去トーナメントの第1段階の実装は簡単です。 たとえば、このような各計算は、ブルートフォース(5つの可能性のそれぞれについて、中間要素であるかどうかを詳細に確認する)または並べ替えの問題に関する情報(セクション6.1.2)を使用して実行できます。 第二段階を実装するために、中央値を計算します
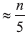
最初のラウンドの勝者は再帰的に。
行1〜2および6〜13は、RSelectアルゴリズムと同じです。 行3〜5は、アルゴリズムの唯一の新しい部分です。 入力配列の中央値の中央値を計算し、参照要素をランダムに選択するRSelectアルゴリズムの行を置き換えます。
3行目と4行目は、ノックアウトトーナメントの第1ラウンドの勝者を計算します。5要素の各グループの中間要素は、検索方法またはソートアルゴリズムを使用して計算され、これらの勝者を新しい配列Cにコピーします。 Cは(仮に)長さを持つため
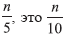
配列Cの-th順序統計。アルゴリズムのどのステップでもランダム化は使用されません。
6.3.3。 DSelectアルゴリズムについて
参照要素を計算する際のDSelectアルゴリズムの再帰呼び出しは、危険なほど循環的に見える場合があります。 何が起こっているのかを理解するために、最初に再帰呼び出しの総数を指定しましょう。
正解は:(c)です。 参照要素が必要な順序統計である基本ケースとハッピーケースを破棄すると、DSelectアルゴリズムは2つの再帰呼び出しを行います。 理由を理解するために、無理をしないでください。 DSelectアルゴリズムの擬似コードを1行ずつ確認するだけです。 行5には1つの再帰呼び出しがあり、行11または13には別の呼び出しがあります。
これらの2つの再帰呼び出しについて、2つの紛らわしい一般的な質問があります。 第一に、RSelectアルゴリズムが再帰呼び出しを1回だけ行うという事実ではありません。これが、ソートアルゴリズムよりも速く動作する理由です。 DSelectは、2つの再帰呼び出しを行うことでこの改善を放棄しませんか? セクション6.4は、5行目の追加の再帰呼び出しが比較的小さなサブタスク(元の配列の要素の20%)のみを解決するため、線形解析を保存できることを示しています。
次に、2つの再帰呼び出しが根本的に異なる役割を果たします。 5行目の再帰呼び出しの目的は、現在の再帰呼び出しの適切な参照要素を決定することです。 11行目または13行目の再帰呼び出しの目標は正常です-現在の再帰呼び出しによって残された小さな残りのタスクを再帰的に解決します。 それでも、DSelectアルゴリズムの再帰構造は、調査した他のすべての分割統治アルゴリズムの伝統に完全に準拠しています。各再帰呼び出しは、厳密に細かいサブタスクで少数の後続の再帰呼び出しを行い、追加の作業を行います。 MergeSortやQuickSortなどのアルゴリズムが永久に実行されることを心配していなければ、DSelectアルゴリズムを心配する必要はありません。
6.3.4。 DSelectアルゴリズムランタイム
DSelectアルゴリズムは、限られた時間で完了する明確に定義されたプログラムではありません。線形時間で実行され、入力データの読み取りに必要な定数よりも多くの作業を行います。
定理6.6(DSelectアルゴリズムの動作時間)。 長さn≥1の各入力配列に対して、DSelectアルゴリズムの動作時間はO(n)です。
原則としてΘ(n2)以下にできるRSelectアルゴリズムの実行時間とは異なり、DSelectアルゴリズムの実行時間は常にO(n)です。 それでも、実際には、最初のものが同じ場所で動作し、定理6.1の平均動作時間「O(n)」に隠れている定数は定理6.6に隠れている定数よりも小さいため、RSelectをDSelectよりも優先する必要があります。
»本の詳細については
、出版社のウェブサイトをご覧ください»
コンテンツ»
抜粋Khabrozhiteleyの場合、クーポンの20%割引-
アルゴリズム本の紙版が支払われると、電子版の本が電子メールで送信されます。
PS:本のコストの7%が新しいコンピューター本の翻訳に費やされ
ます 。印刷会社に渡された本のリストは
こちらです。