ジュリアからの6人の予想外の男性

最後に、 ロシア語のジュリア言語ガイドが登場しました。 プログラミングの経験がほとんどない人のために言語の完全な紹介を提供します（残りは一般的な開発に役立ちます）。また、機械学習の紹介と、資料を統合するための一連のタスクもあります。

検索中に、 経済学者向けのプログラミングコースに出会いました（ジュリアに加えて、Pythonもあります）。 経験豊富な方は、 クイックコースに進むか、「 コンピュータサイエンティストのように考える方法」という本を読むことができます。

以下は、ブログChristopher Rackauckas 7 Julia Gotchasの資料の翻訳とその取り扱い方法です。

まず、ジュリアは素晴らしい言語だと言ってみましょう。 私は彼女が大好きです。これは私が今まで使用した中で最も強力で直感的な言語だと考えています。 これは間違いなく私のお気に入りの言語です。 ただし、知っておく必要がある「落とし穴」がいくつかあります。 各言語にはそれらがあります。言語を習得するために最初にしなければならないことの1つは、それらが何であるか、およびそれらを回避する方法を見つけることです。 この投稿のポイントは、代替のプログラミング方法を示唆する最も一般的ないくつかを明らかにすることにより、このプロセスをスピードアップするのに役立つことです。

ジュリアは何が起きているのかを理解するのに適した言語です。なぜなら、魔法はそこにないからです。 ジュリアの開発者は、行動規則を明確に定義したいと考えていました。 これは、すべての動作を説明できることを意味します。 ただし、これは、1つのことが正確に起こり、別のことが起こらない理由を理解するために頭を痛めなければならないことを意味する場合があります。 そのため、いくつかの一般的な問題を説明するだけでなく、それらが発生する理由についても説明します。 いくつかの非常に類似したパターンがあり、それらに気づくとすぐに、それらのいずれかから外れることはなくなります。 このため、Juliaの学習曲線は、 MATLAB / R / Pythonのような単純な言語に比べてわずかに急勾配です 。 ただし、これを習得すると、Juliaの簡潔さを完全に活用して、 C / Fortranのパフォーマンスを得ることができます。 さらに深く掘り下げます。

予期しない時間：REPL（端末）にはグローバルスコープがあります

これは、新しいジュリアユーザーによって報告された最も一般的な問題です。 誰かが言う：「聞いた、ジュリアは速い！」、REPLを開き、すぐに有名なアルゴリズムを書き留めて、このスクリプトを実行する。 実行後、彼らは時間を見て、「ちょっと待って、なぜPythonのように遅いのですか？」と言います。 これは非常に重要で一般的な問題であるため、これを回避する方法を理解するために、これが起こる理由を調査するために時間を費やしましょう。

小さな余談：ジュリアが速い理由

Juliaはコードのコンパイルだけでなく、型の特殊化（つまり、これらの型に固有のコードのコンパイル）でもあることを理解する必要があります。 繰り返しますが、コードはJITコンパイラーを使用してコンパイルされるため、Juliaは高速ではありません。むしろ、速度の秘密は型固有のコードがコンパイルされることです。

完全なストーリーが必要な場合は、次回のセミナーのために私が書いたメモをご覧ください 。 型の特異性は、ジュリアの設計の基本原則である多重ディスパッチによって決定されます。 コードを書くとき：

 function f(a,b) return 2a+b end 

これは1つのにすぎないようですが、実際には、ここで多数のが作成されています。 ジュリアの言語では、関数は抽象化であり、実際に呼び出されるのはメソッドです。 f(2.0,3.0)を呼び出すと、Juliaはコンパイルされたコードを実行します。このコードは2つの浮動小数点数を取り、 2a + bを返します。 f(2,3)を呼び出すと、ジュリアは2つの整数を取り、 2a + bを返す別のコンパイル済みコードを実行します。 関数fは、同じ形式を持つ多くの異なるメソッドの抽象化または略語であり、シンボルfを使用してこれらすべての異なるメソッドを呼び出すような方式は、複数ディスパッチと呼ばれます。 そして、これはどこにでも当てはまります。 +演算子は、実際には、表示される型に応じてメソッドを呼び出す関数です。 彼女がコンパイルしたコードは彼女の型を知っているので、実際にジュリアは彼女の速度を取得します。したがって、f（2.0,3.0）を呼び出すコンパイル済みコードは、 C / Fortranで同じ関数を定義することで得られるコンパイル済みコードです。 これをcode_nativeマクロで確認して、コンパイルされたアセンブリを確認できます。

 @code_native f(2.0,3.0) 

 pushq %rbp movq %rsp, %rbp Source line: 2 vaddsd %xmm0, %xmm0, %xmm0 vaddsd %xmm1, %xmm0, %xmm0 popq %rbp retq nop 

これは、 C / Fortranの関数から期待されるものと同じコンパイル済みアセンブリであり、整数のアセンブリコードとは異なります。

 @code_native f(2,3) pushq %rbp movq %rsp, %rbp Source line: 2 leaq (%rdx,%rcx,2), %rax popq %rbp retq nopw (%rax,%rax) 

本質：REPL /グローバルスコープは型の特異性を許可しません

これにより、主なポイントがわかります。REPL/グローバルスコープは、型の指定が許可されていないため低速です。 まず、ジュリアは関数のネストされたスコープを許可するため、REPLはグローバルスコープであることに注意してください。 たとえば、定義する場合

 function outer() a = 5 function inner() return 2a end b = inner() return 3a+b end 

このコードが機能することがわかります。 これは、Juliaを使用すると、外部関数から内部関数にキャプチャできるためです。 この考え方を再帰的に適用すると、最も高い領域が直接REPLである領域（ メインモジュールのグローバルスコープ）であることがわかります。 しかし、この状況で関数がどのようにコンパイルされるかを考えてみましょう。 同じことを実装しますが、グローバル変数を使用します。

 a=2.0; b=3.0 function linearcombo() return 2a+b end ans = linearcombo() 

そして

 a = 2; b = 3 ans2= linearcombo() 

質問：コンパイラはaとbに対してどの型を受け入れるべきですか？ この例では、型を変更しても同じ関数が呼び出されることに注意してください。 浮動、整数、配列、奇妙なユーザー型など、追加する任意の型を処理できます。Julia言語では、変数をボックス化する必要があり、使用するたびに型がチェックされます。 コンパイルされたコードはどのように見えると思いますか？

 pushq %rbp movq %rsp, %rbp pushq %r15 pushq %r14 pushq %r12 pushq %rsi pushq %rdi pushq %rbx subq $96, %rsp movl $2147565792, %edi # imm = 0x800140E0 movabsq $jl_get_ptls_states, %rax callq *%rax movq %rax, %rsi leaq -72(%rbp), %r14 movq $0, -88(%rbp) vxorps %xmm0, %xmm0, %xmm0 vmovups %xmm0, -72(%rbp) movq $0, -56(%rbp) movq $10, -104(%rbp) movq (%rsi), %rax movq %rax, -96(%rbp) leaq -104(%rbp), %rax movq %rax, (%rsi) Source line: 3 movq pcre2_default_compile_context_8(%rdi), %rax movq %rax, -56(%rbp) movl $2154391480, %eax # imm = 0x806967B8 vmovq %rax, %xmm0 vpslldq $8, %xmm0, %xmm0 # xmm0 = zero,zero,zero,zero,zero,zero,zero,zero,xmm0[0,1,2,3,4,5,6,7] vmovdqu %xmm0, -80(%rbp) movq %rdi, -64(%rbp) movabsq $jl_apply_generic, %r15 movl $3, %edx movq %r14, %rcx callq *%r15 movq %rax, %rbx movq %rbx, -88(%rbp) movabsq $586874896, %r12 # imm = 0x22FB0010 movq (%r12), %rax testq %rax, %rax jne L198 leaq 98096(%rdi), %rcx movabsq $jl_get_binding_or_error, %rax movl $122868360, %edx # imm = 0x752D288 callq *%rax movq %rax, (%r12) L198: movq 8(%rax), %rax testq %rax, %rax je L263 movq %rax, -80(%rbp) addq $5498232, %rdi # imm = 0x53E578 movq %rdi, -72(%rbp) movq %rbx, -64(%rbp) movq %rax, -56(%rbp) movl $3, %edx movq %r14, %rcx callq *%r15 movq -96(%rbp), %rcx movq %rcx, (%rsi) addq $96, %rsp popq %rbx popq %rdi popq %rsi popq %r12 popq %r14 popq %r15 popq %rbp retq L263: movabsq $jl_undefined_var_error, %rax movl $122868360, %ecx # imm = 0x752D288 callq *%rax ud2 nopw (%rax,%rax) 

型の特殊化を行わない動的言語の場合、余分な命令をすべて含むこの肥大化したコードは可能な限り優れているため、Juliaは速度が低下します。 これが非常に重要である理由を理解するには、Juliaで記述する各コードがコンパイルされることに注意してください。 スクリプトにループを書いたとしましょう：

 a = 1 for i = 1:100 a += a + f(a) end 

コンパイラーはこのループをコンパイルする必要がありますが、型が変更されないことを保証できないため、保守的にすべての型でフットクロスをラップし、実行が遅くなります。

問題を回避する方法

この問題を回避する方法はいくつかあります。 最も簡単な方法は、スクリプトを関数で常にラップすることです。 たとえば、前のコードの形式は次のとおりです。

 function geta(a) # can also just define a=1 here for i = 1:100 a += a + f(a) end return a end a = geta(1) 

これにより同じ結果が得られますが、コンパイラーはa型に特化できるため、必要なコンパイル済みコードを提供します。 もう1つできることは、変数を定数として定義することです。

 const b = 5 

これを行うことにより、変数が変更されないことをコンパイラーに伝えるため、現在使用されている型で変数を使用するすべてのコードを特殊化することができます。 ジュリアでは、定数ではなく型の値を実際に変更できるというちょっとした癖があります。 そうすれば、 constを使用して、型を変更しないことをコンパイラーに伝えることができます。 ただし、いくつかの小さな癖があることに注意してください。

 const a = 5 f() = a println(f()) # Prints 5 a = 6 println(f()) # Prints 5 # WARNING: redefining constant a 

コンパイラーは、 f () = a （ aは定数であるためf () = aへの答えを知っていることを認識して、関数呼び出しを答えに置き換え、 a定数でない場合a異なる動作をするため、期待どおりに動作しません。

道徳：スクリプトをREPLで直接書くのではなく、常に関数でラップしてください。

Nezhdanchik 2：タイプの不安定性

そのため、データ型にとってコードの特殊化がいかに重要であるかについて意見を述べたところです。 質問をさせてください。あなたのタイプが変わるとどうなりますか？ 「この場合、コンパイルされたコードを専門化することはできません」と推測した場合、あなたは正しいです。 このような問題は、型の不安定性として知られています。 これらはさまざまな方法で表示できますが、一般的な例の1つは、単純に値を初期化することです。 たとえば、次を見てみましょう。

 function g() x=1 for i = 1:10 x = x/2 end return x end 

1/2はJuliaの浮動小数点数であることに注意してください。 したがって、 x = 1で開始した場合、整数は浮動小数点数に変更されるため、関数は、内部ループをコンパイルして、任意の型であるかのようにする必要があります。 代わりにあった場合：

 function h() x=1.0 for i = 1:10 x = x/2 end return x end 

次に、 xが浮動小数点数のままであることを知って、関数全体が最適にコンパイルできるようになります（コンパイラーが型を判別するこの機能を型推論と呼びます）。 コンパイルされたコードをチェックして、違いを確認できます。

 pushq %rbp movq %rsp, %rbp pushq %r15 pushq %r14 pushq %r13 pushq %r12 pushq %rsi pushq %rdi pushq %rbx subq $136, %rsp movl $2147565728, %ebx # imm = 0x800140A0 movabsq $jl_get_ptls_states, %rax callq *%rax movq %rax, -152(%rbp) vxorps %xmm0, %xmm0, %xmm0 vmovups %xmm0, -80(%rbp) movq $0, -64(%rbp) vxorps %ymm0, %ymm0, %ymm0 vmovups %ymm0, -128(%rbp) movq $0, -96(%rbp) movq $18, -144(%rbp) movq (%rax), %rcx movq %rcx, -136(%rbp) leaq -144(%rbp), %rcx movq %rcx, (%rax) movq $0, -88(%rbp) Source line: 4 movq %rbx, -104(%rbp) movl $10, %edi leaq 477872(%rbx), %r13 leaq 10039728(%rbx), %r15 leaq 8958904(%rbx), %r14 leaq 64(%rbx), %r12 leaq 10126032(%rbx), %rax movq %rax, -160(%rbp) nopw (%rax,%rax) L176: movq %rbx, -128(%rbp) movq -8(%rbx), %rax andq $-16, %rax movq %r15, %rcx cmpq %r13, %rax je L272 movq %rbx, -96(%rbp) movq -160(%rbp), %rcx cmpq $2147419568, %rax # imm = 0x7FFF05B0 je L272 movq %rbx, -72(%rbp) movq %r14, -80(%rbp) movq %r12, -64(%rbp) movl $3, %edx leaq -80(%rbp), %rcx movabsq $jl_apply_generic, %rax vzeroupper callq *%rax movq %rax, -88(%rbp) jmp L317 nopw %cs:(%rax,%rax) L272: movq %rcx, -120(%rbp) movq %rbx, -72(%rbp) movq %r14, -80(%rbp) movq %r12, -64(%rbp) movl $3, %r8d leaq -80(%rbp), %rdx movabsq $jl_invoke, %rax vzeroupper callq *%rax movq %rax, -112(%rbp) L317: movq (%rax), %rsi movl $1488, %edx # imm = 0x5D0 movl $16, %r8d movq -152(%rbp), %rcx movabsq $jl_gc_pool_alloc, %rax callq *%rax movq %rax, %rbx movq %r13, -8(%rbx) movq %rsi, (%rbx) movq %rbx, -104(%rbp) Source line: 3 addq $-1, %rdi jne L176 Source line: 6 movq -136(%rbp), %rax movq -152(%rbp), %rcx movq %rax, (%rcx) movq %rbx, %rax addq $136, %rsp popq %rbx popq %rdi popq %rsi popq %r12 popq %r13 popq %r14 popq %r15 popq %rbp retq nop 

に対して

 pushq %rbp movq %rsp, %rbp movabsq $567811336, %rax # imm = 0x21D81D08 Source line: 6 vmovsd (%rax), %xmm0 # xmm0 = mem[0],zero popq %rbp retq nopw %cs:(%rax,%rax) 

同じ値を取得するための計算数のこのような違い！

型の不安定性を見つけて対処する方法

この時点で、「さて、なぜCを使用してこれらの不安定性を探す必要がないのですか？」と尋ねることができます。 答えは：

1. 見つけやすい
2. 彼らは役に立つかもしれません。

3. 機能的な障壁で不安定に対処できます

   
   

   Juliaはcode_warntypeマクロを提供して、型の不安定性の場所を示します。 たとえば、作成したg関数でこれを使用すると、次のようになります。

   
   

    @code_warntype g() 

   
   

 Variables: #self#::#g x::ANY #temp#@_3::Int64 i::Int64 #temp#@_5::Core.MethodInstance #temp#@_6::Float64 Body: begin x::ANY = 1 # line 3: SSAValue(2) = (Base.select_value)((Base.sle_int)(1,10)::Bool,10,(Base.box)(Int64,(Base.sub_int)(1,1)))::Int64 #temp#@_3::Int64 = 1 5: unless (Base.box)(Base.Bool,(Base.not_int)((#temp#@_3::Int64 === (Base.box)(Int64,(Base.add_int)(SSAValue(2),1)))::Bool)) goto 30 SSAValue(3) = #temp#@_3::Int64 SSAValue(4) = (Base.box)(Int64,(Base.add_int)(#temp#@_3::Int64,1)) i::Int64 = SSAValue(3) #temp#@_3::Int64 = SSAValue(4) # line 4: unless (Core.isa)(x::UNION{FLOAT64,INT64},Float64)::ANY goto 15 #temp#@_5::Core.MethodInstance = MethodInstance for /(::Float64, ::Int64) goto 24 15: unless (Core.isa)(x::UNION{FLOAT64,INT64},Int64)::ANY goto 19 #temp#@_5::Core.MethodInstance = MethodInstance for /(::Int64, ::Int64) goto 24 19: goto 21 21: #temp#@_6::Float64 = (x::UNION{FLOAT64,INT64} / 2)::Float64 goto 26 24: #temp#@_6::Float64 = $(Expr(:invoke, :(#temp#@_5), :(Main./), :(x::Union{Float64,Int64}), 2)) 26: x::ANY = #temp#@_6::Float64 28: goto 5 30: # line 6: return x::UNION{FLOAT64,INT64} end::UNION{FLOAT64,INT64} 

最初は、タイプxがAnyと言うことに注意してください。 strict typeとして指定されていないstrict type 、つまり、各ステップでボックス化/チェックする必要がある抽象タイプです。 最終的にxをUNION {FLOAT64, INT64}として返します。これは別の非厳密型です。 これにより、タイプが変更され、問題が生じていることがわかります。 代わりにh code_warntypeを見ると、すべての厳密な型を取得します。

 @code_warntype h() Variables: #self#::#h x::Float64 #temp#::Int64 i::Int64 Body: begin x::Float64 = 1.0 # line 3: SSAValue(2) = (Base.select_value)((Base.sle_int)(1,10)::Bool,10,(Base.box)(Int64,(Base.sub_int)(1,1)))::Int64 #temp#::Int64 = 1 5: unless (Base.box)(Base.Bool,(Base.not_int)((#temp#::Int64 === (Base.box)(Int64,(Base.add_int)(SSAValue(2),1)))::Bool)) goto 15 SSAValue(3) = #temp#::Int64 SSAValue(4) = (Base.box)(Int64,(Base.add_int)(#temp#::Int64,1)) i::Int64 = SSAValue(3) #temp#::Int64 = SSAValue(4) # line 4: x::Float64 = (Base.box)(Base.Float64,(Base.div_float)(x::Float64,(Base.box)(Float64,(Base.sitofp)(Float64,2)))) 13: goto 5 15: # line 6: return x::Float64 end::Float64 

これは、関数の型が安定しており、基本的に最適なCコードにコンパイルされることを示しています 。 したがって、型の不安定性を見つけるのは難しくありません。 さらに難しいのは、適切なデザインを見つけることです。 型の不安定性を解決する理由 これは、動的に型付けされた言語がスクリプトの分野を支配しているという事実につながった長年の問題です。 多くの場合、パフォーマンスと信頼性の妥協点を見つけたいと考えています。

たとえば、整数が浮動小数点数と混合されているWebページからテーブルを読み取ることができます。 Juliaでは、関数がすべて整数である場合は適切にコンパイルされ、すべて浮動小数点数である場合も適切にコンパイルされるように関数を記述できます。 そして、それらが混在している場合は？ これは引き続き機能します。 これは、 Python / Rのような言語から私たちが知っていて愛している柔軟性/便利さです。 ただし、パフォーマンスを犠牲にする場合、Juliaは（ code_warntypeを介して ）直接通知します。

型の不安定性に対処する方法

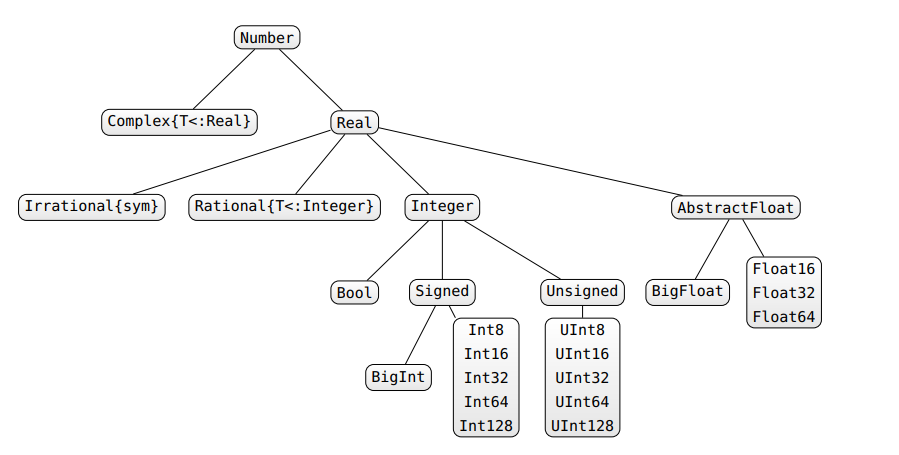
型の不安定性に対処するには、いくつかの方法があります。 まず、型が宣言されていて変更できない（型の安定性を確保する） C / Fortranのようなものが好きな場合は、Juliaでこれを行うことができます。

 local a::Int64 = 5 

これにより64ビット整数が作成され、将来のコードで変更しようとすると、エラーメッセージが生成されます（または正しい変換が実行されます。ただし、変換は自動的に丸められないため、エラーが発生する可能性が高くなります）。 コードにそれらを振りかけると、型安定性、ala、 C / Fortranが得られます。 これを処理するそれほど複雑でない方法は、typeステートメントを使用することです。 ここでは、等号の反対側に同じ構文を配置します。 例：

 a = (b/c)::Float64 

「b / cを計算し、出力がFloat64であることを確認してください。そうでない場合は、自動変換を実行してください。変換を簡単に実行できない場合は、エラーを出力してください。」 このようなデザインを配置すると、どのタイプが関係しているかを確認するのに役立ちます。 ただし、場合によっては、型の不安定性が必要です。 たとえば、信頼性の高いコードを持ちたいが、ユーザーが次のようなおかしなものを与えたとします。

 arr = Vector{Union{Int64,Float64}}(undef, 4) arr[1]=4 arr[2]=2.0 arr[3]=3.2 arr[4]=1 

これは、4x1整数と浮動小数点数の配列です。 配列の実際の要素タイプはUnion {Int64, Float64} 、これは先ほど見たように厳密ではなく、問題を引き起こす可能性がありました。 コンパイラーは、各値が整数または浮動小数点数であることのみを認識しますが、どのタイプの要素ではないことを認識します。 これは、この配列を使用して算術を行うのが単純であることを意味します。たとえば、次のとおりです。

 function foo{T,N}(array::Array{T,N}) for i in eachindex(array) val = array[i] # do algorithm X on val end end 

操作がボックス化されるため、遅くなります。 ただし、複数のディスパッチを使用して、特別な方法でコードを実行できます。 これは、機能バリアの使用として知られています。 例：

 function inner_foo{T<:Number}(val::T) # Do algorithm X on val end function foo2{T,N}(array::Array{T,N}) for i in eachindex(array) inner_foo(array[i]) end end 

複数のディスパッチにより、 inner_foo呼び出すと、浮動小数点数用に特別にコンパイルされたメソッドまたは整数用に特別にコンパイルされたメソッドが呼び出されます。 したがって、 inner_foo長い計算を入れても、機能バリアが提供する厳密な型付けに劣らず、うまく機能することができます。

したがって、Juliaが強力なタイピングパフォーマンスと動的なタイピングの便利さの優れた組み合わせを提供していることをご確認ください。 優れたプログラマー、ジュリアは、生産性および/または必要に応じて生産性を最大化するために、両方を自由に使用できます。

サプライズ3：Evalはグローバルに機能します

ジュリアの最大の強みの1つは、メタプログラミング機能です。 これにより、コード生成プログラムを簡単に記述でき、記述および保守する必要があるコードの量を効果的に削減できます。 マクロは、コンパイル時に実行され、（通常）コードを吐き出す関数です。 例：

 macro defa() :(a=5) end 

defaインスタンスをコードa = 5で置き換えます（ :(a = 5)は引用符で囲まれた式です。ジュリアのコードは式であるため、メタプログラミングは式のコレクションです）。

これを使用して、希望する複雑なジュリアプログラムを作成し、一種の非常にスマートなショートカットとして関数に入れることができます。 ただし、生成されたコードを直接評価する必要がある場合があります。 Juliaは、これを行うためのeval関数または@evalマクロを提供します。 一般に、 evalを避けるようにする必要がありますが、たとえば、 並列プログラミングの異なるプロセス間でデータを転送するための新しいライブラリなど、必要なコードがいくつかあります 。 , , :

 @eval :(a=5) 

(REPL). , / . 例：

 function testeval() @eval :(a=5) return 2a+5 end 

, a REPL. , , :

 function testeval() @eval :(a=5) b = a::Int64 return 2b+5 end 

b — , , , , , . eval , , REPL .

4:

Julia , . : , .

, ? , , . 例：

 a = 2 + 3 + 4 + 5 + 6 + 7 +8 + 9 + 10+ 11+ 12+ 13 a 

, 90, 27. ? a = 2 + 3 + 4 + 5 + 6 + 7 , a = 27 , +8 + 9 + 10+ 11+ 12+ 13 , , , :

 a = 2 + 3 + 4 + 5 + 6 + 7 + 8 + 9 + 10+ 11+ 12+ 13 

90, . , .

. — , . rssdev10

. 例：

 x = rand(2,2) a = [cos(2*pi.*x[:,1]).*cos(2*pi.*x[:,2])./(4*pi) -sin(2.*x[:,1]).*sin(2.*x[:,2])./(4)] b = [cos(2*pi.*x[:,1]).*cos(2*pi.*x[:,2])./(4*pi) - sin(2.*x[:,1]).*sin(2.*x[:,2])./(4)] 

, a b — , ! (2,2) , — (1-) 2. , , :

 a = [1 -2] b = [1 - 2] 

: 1 -2 . : 1-2 . - . :

 a = [1 2 3 -4 2 -3 1 4] 

2x4. , . : hcat :

 a = hcat(cos(2*pi.*x[:,1]).*cos(2*pi.*x[:,2])./(4*pi),-sin(2.*x[:,1]).*sin(2.*x[:,2])./(4)) 

!

№5: ,

(View) — () , ( ), .

, , . , . , .

— "". "" , . "" — ( ). ( () ) . , :

 a = [3;4;5] b = a b[1] = 1 

, a — [1; 4; 5] , . . b a . , b = a b a . , , b , , ( b a ). , . , , :

 a = rand(2,2) # Makes a random 2x2 matrix b = vec(a) # Makes a view to the 2x2 matrix which is a 1-dimensional array 

b , b a , b . , , ( , ). . , . 例：

 c = a[1:2,1] 

( , c a ). , , , , . , , :

 d = @view a[1:2,1] e = view(a,1:2,1) 

d , e — , d e a , , , . ( , , — reshape , .) , . 例：

 a[1:2,1] = [1;2] 

a , a[1:2,1] view (a, 1:2,1) , , a . -? , :

 b = copy(a) 

, b a , , b a . a , copy! (B, a) , a a ( , b ). . , Vector {Vector} :

 a = [ [1, 2, 3], [4, 5], [6, 7, 8, 9] ] 

. , ?

 b = copy(a) b[1][1] = 10 a 

 3-element Array{Array{Int64,1},1}: [10, 2, 3] [4, 5] [6, 7, 8, 9] 

, a[1][1] 10! なぜこれが起こったのですか？ copy a . a , b , b . , deepcopy :

 b = deepcopy(a) 

, . , , .

№6: , In-Place

MATLAB / Python / R . Julia , , , " ". (. . , , , , ). (in-place), . ? in-place ( mutable function ) — , , . , . , :

 function f() x = [1;5;6] for i = 1:10 x = x + inner(x) end return x end function inner(x) return 2x end 

, inner , , 2x . , . , - y , :

 function f() x = [1;5;6] y = Vector{Int64}(3) for i = 1:10 inner(y,x) for i in 1:3 x[i] = x[i] + y[i] end copy!(y,x) end return x end function inner!(y,x) for i=1:3 y[i] = 2*x[i] end nothing end 

. inner!(y, x) , y . y , y , , , inner! (y, x) . , , mutable (, ""). ! ( ).

, inner!(y, x) . copy!(y, x) — , x y , . , , . : x y . , x + inner(x) , , , 11 . , .

, , , . - ( loop-fusion ). Julia v0.5 . ( ( broadcast ), ). , f.(x) — , f x , , . f x , x = x + f. (x) . :

 x .= x .+ f.(x) 

.= , , ,

 for i = 1:length(x) x[i] = x[i] + f(x[i]) end 

, :

 function f() x = [1;5;6] for i = 1:10 x .= x .+ inner.(x) end return x end function inner(x) return 2x end 

MATLAB / R / Python , , , . , , C / Fortran .

: ,

: , . , . , . , , . , .

- , C / Fortran , . - , , !

: ? , . , , ? [ , Javascript var x = 3 x , x = 3 x . ? , - Javascript!]