ほぼ10年前、私は素晴らしい物理学者および哲学者である
Max Tegmarkの 記事を読み
、その中に私の人生を苦しめてきた多くの質問への答えを見つけました。 この記事は驚くべきもので、2か月間その印象を受けました。 残念ながら、これはLongridであり、英語でもあります。 したがって、私はそれを翻訳することさえしないことにしました-翻訳はまだHabrにとって長すぎますが、少なくとも私にとって論理的に見える順序で主要なアイデアを設定し、不必要な詳細を削除します（マックスは許して！）
フォーミュラと手荷物
これは何ですか この式は、あなたに何も伝えないでしょう。 そして、このように書くと：
その後、すぐにニュートンの法則を認識します。 もちろん、両方の式は同等であり、力がF、質量mで示されるという事実に慣れているだけでなく、物質が3次元空間で発生すること、物体に座標があることなどを意味します。 つまり、理論には2つの要素があります。それは、式とその周りの
なんとかです。 Maxは、2番目のコンポーネントの
口頭荷物を呼び出します。
既存の理論の木を考えてみましょう：
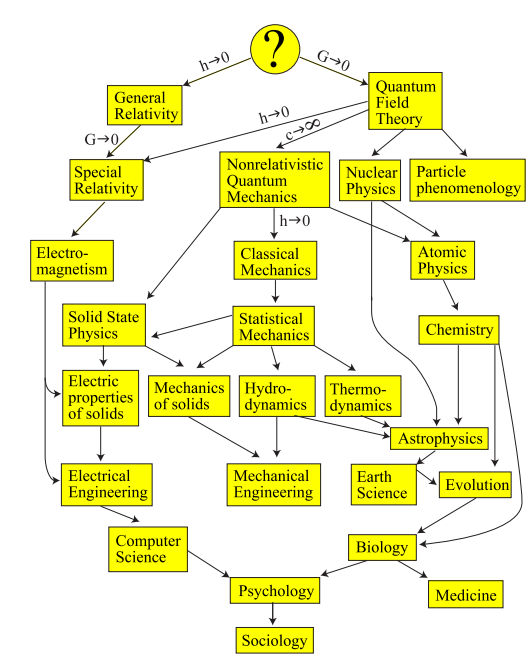
一番下にあるのは社会学であり、そこではほとんど公式はないが、多くの言葉がある。 2階に移動すると、ますます複雑な数学に遭遇します。 しかし、言葉ではますます悪化しています。基礎物理学に携わっている科学者に何時かを調べてみてください。 時間は
一連の出来事であり、それが
前進することはあなたには明らか
です 。 知れば知るほど、深くなればなるほど、わかりにくくなります。 時が何であるかの説明は、時間が文字
tであるという事実にますます崩壊します。文字
tは 、そのような方程式に関係しています。
マックスは次のことに気付きます。
ますます基本的なレベルに移行すると、数学はより複雑になり、荷物はますます退化し始めます。 限界では、マックスは、TOE（すべての理論-すべての一般的な理論）には荷物がないことを示唆しています。 したがって、 TOEは式のみで構成されます 。これが最初の材料です。 彼を覚えている。
物理学「反対に」
これはどのように可能ですか？ 物理学は、観測と実験データに基づいて、私たちの世界の方程式を見つけようとしています。 マックスは「
スクラッチからの物理学 」を見ることを提案します-「方程式を設定します、あなたはどんな種類の世界を手に入れますか？」
私たちは世界の法則を設定することができます...まあ、たとえば、ゲーム「人生」。 言葉による説明なしでできますか？ たとえば、細胞の空間が2次元であると言うにはどうすればよいでしょうか？ 方程式を通じて、べき乗則を示すことにより、セルの数がどれだけ速く距離Nを超えて成長するか。別の例では
、弦理論の
方程式は 、空間の次元が10、11、または26の場合にのみ収束します。公理理論（および世界）を作成します。 たとえば、
ペアノの
公理論を考えてみましょう。 これらは純粋な式であり、「数値」とは何か、加算または乗算することの意味は説明していません。
説明と同等。
何がありますか？ 存在するすべてを記述するTOEを持っています（します）。
1秒...そして、「説明」とはどういう意味ですか？ たとえば、力学は体の動きを表します。 しかし、多くの単純化のおかげでこれがすべて可能であることを知っています：ボディは重要なポイントではなく、空気抵抗、摩擦などがあります。 現実を記述する式はありますが、現実の世界は、式で表される理想とは異なることを知っています。
しかし、TOEの場合、これはそうではありません。現実の物理的側面はすべて、公式によって記述されます-または、TOEではありません。 この場合、理論と現実の違いは何ですか？
マックスは、TOEの場合、
数学は現実を説明せず、数学は現実であると主張します。 あなたが突然同意しない場合、反対はその解を伴う方程式が存在することを意味します。示された式の完全に対象となるのとまったく同じ世界が存在します。 この場合、「
まだ本物 」という
言葉は、純粋な形の
言葉による荷物であり、上記のように放棄した
、物理学のような現代の
アニマソラです。 したがって、
基本レベルでは、物理学と数学はまったく同じであることを認めざるを得
ません。フォーミュラと炎
マックスはそのようなアイデアを持つ最初ではありませんでした。 ホーキング自身が問題を提起しました：「
しかし、炎はこれらの方程式に正確に息を吹き込み、宇宙を作り出しますか？」 」
「方程式に火を吹き込み、それらを記述するための宇宙を作るのは何ですか？」
私たちの宇宙が
存在しているために特別で
あると言った場合 、再びアニマ・ソラの概念に一歩戻されます。 いいえ、フォーミュラに炎を吹き込むものは何もありません。 数学のすべての公理体系が、宇宙が存在するシステムと不運なシステムの2つの不均等なクラスに分割されるとしたら、奇妙です。 これは、数学的宇宙の仮説全体と矛盾しています。
これはすべてこの方法でしか説明できません。アニマソラがない場合、
すべての公理系は等しく、宇宙は
各公理系に対応します。 はい、ほとんどのシステムは自明である可能性が高く、おそらくほとんどの公理学は複雑で自明でないシステム、特に生命を開発する（つまり、ソリューションに登場する）機会を与えません。
「物理はその逆」は、まだ将来の研究者を待っています。 私たちの宇宙は、知的生命が可能なものの中で最も単純なものであるかどうかを知るために心からお願いします。
いくつかの質問への回答
興味深いことに、最初のステップ（TOUには荷物がありません）の後、2番目のステップ（数学と物理学はまったく同じです）と3番目のステップ（各公理学は宇宙を作ります）が強制されました。 それは私たちが得た距離です。
そして、なぜ宇宙は存在するのでしょうか？
回答：
存在できるからです。これらの構造はいつ発生し、なぜ発生したのですか？
数学的構造は時間と空間に存在しません。 それらはただ存在します。
エミュレーションですか？
いや 数学的構造が存在する場合、それらを「数える」ための機械は必要ありません。 数字の19は、常にサイクルを分割しようとするコンピューターがあるかどうかに関係なく単純であり、単純さを確認します
そして、これは一般的に科学や空想に似ていますか？
基本的に検証できないものをどのように仮定できますか？ マックスはこの批判を期待しています。 実際、これを行うのはこれが初めてではありません。 私たちは長い間、多元宇宙の概念に慣れてきました。
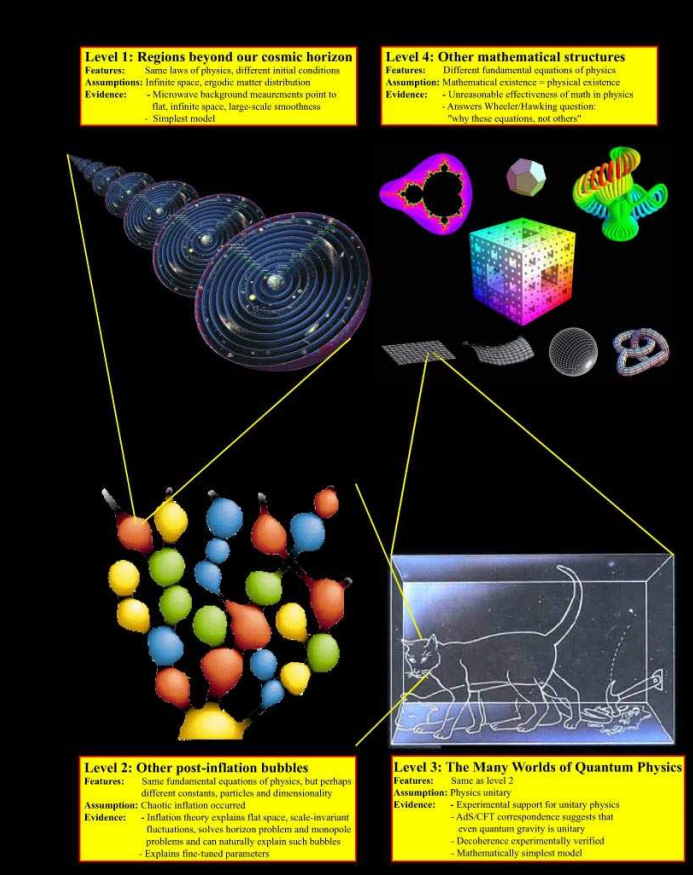レベル1では、膨張のために私たちから非常に急速に遠ざかる宇宙の領域について話します。 それにもかかわらず、宇宙飛行士が一人も舌を回してそこに何もないと言うことはありません。
レベル2では、 永遠のインフレーションの理論における他の「バブル」について話します。おそらく、同じ物理法則、その他の初期条件、その他の物理定数の下で
レベル3は 、エベレットが解釈した多元宇宙の代替宇宙によって形成されます。 これは別の記事になります。
まだ研究していない他の数学的宇宙に対応する
レベル4の存在を理論的に受け入れ
ざるを得ません。