無理数のフラクタル。 パート2

パート0： 素数のフラクタル。
パート1： 無理数のフラクタル。



この記事にはGifと対照的な画像が含まれています。 てんかんはてんかん発作を起こすことがあります。

前回の記事では、バイナリシーケンス可視化アルゴリズムについて説明しました。 覚えておきましょう。

バイナリシーケンスを取得します。 例として、前の記事で説明したフラクタルシーケンスの最初の数ビット：

$$

$$Q_n = \ lfloor n \ sqrt {2} \ rfloor \; （\ textrm {mod} \; 2）; \ quad n = 0,1,2、...$$

0100110110010011001001101100

正方形のセルフィールドを描画します。 ビットを上限に設定します。 ビット間の距離は2セルです。



ビットごとに、対角線に沿って（セルを通る）破線のパスを描画します。 ゼロの場合、最初のストロークを右に描画します。



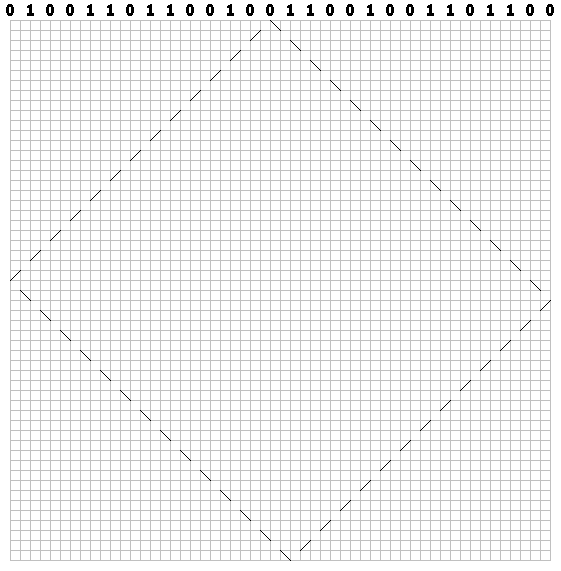
ユニットの場合-左へ：



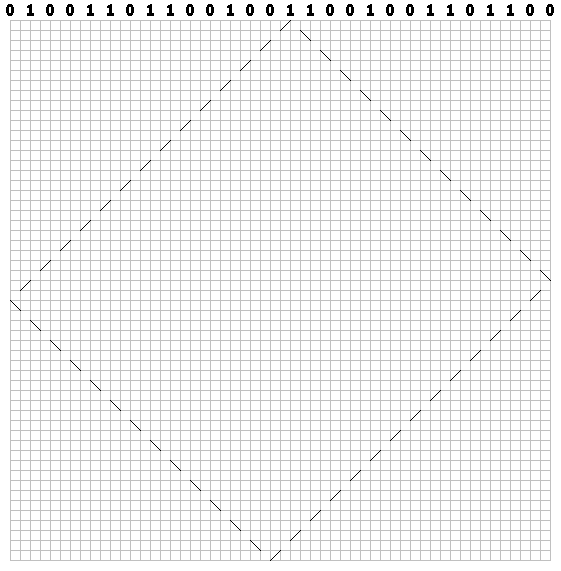
ビットごとに軌跡を描きます。 「ビリヤード」パターンを取得しました。



同じパターン（斜めの欠陥なし-シーケンスは無限、最終シーケンスとして視覚化）は別の方法で取得できます。 シーケンスのすべての偶数ビットを反転します。

0 0 0 1 1 0 0 0 1 1 0 0 0 1 1 0 0 1 1 1 0 0 1 1 1 0 0 1

次に、ビットごとに、垂直の破線を描画します。



ビットを左側に配置し、水平線を描画します。



私たちは結合します：



最初の記事を書いた後、2つの質問が未解決のままでした。

1.無理数のフラクタルパターンを描くことは可能ですか。 できます。 この問題は前の記事で解決されました。 上の写真では-のフラクタルパターンの一部 $$$\ sqrt {2}$。 このパターンで曲線の1つを選択した場合：



有名なフラクタル曲線-「フィボナッチワードフラクタル」を取得します。

2. 2番目の質問は、パターンをペイントするアルゴリズムを作成できるかどうかです。



2番目の問題はこの記事で対処します。 JavaScriptを使用して動作をシミュレートする織機を使用して、パターンに色を付けます。



上の図では-最も簡単なマシンです。 スレッドが引き伸ばされる2つのフレームで構成されます。 フレームはペダルに接続されています。 ペダルの1つを押すと、フレームの1つが上がります。 このフレームを通して引き出された糸は上昇し、横糸が結果として生じる糸の間の隙間に引き伸ばされます。 偶数フレームと奇数スレッドを異なるフレームに引き伸ばすと、チェッカーボードパターンの織りが得られます。



より複雑なマシンでは、4つ以上のフレームが使用されます。


アシュフォード4シャフトテーブルルーム

どのペダルを踏むのか混乱しないように、図を作成します。



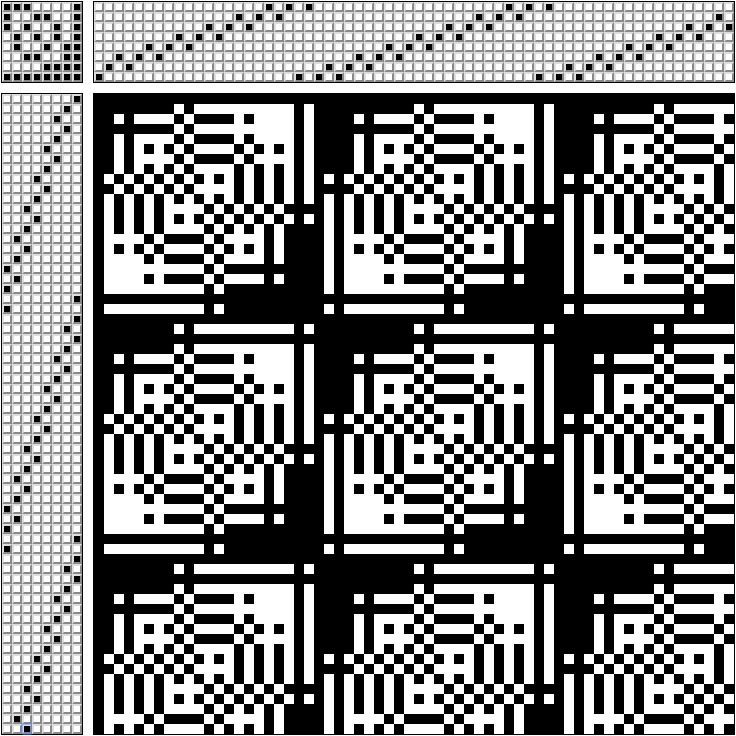
パターンの右上部分には、スレッドがどのフレームを通過するかが示されます（8フレーム織機のパターン）。

左上隅-同時にクランプするペダル（各ペダルは独自のフレームでのみ接続されます）。

左下部分-ペダルを踏む順番。

右下-織り方 白い糸を黒に引き伸ばすと、モノクロパターンが得られます。

すぐに原則を「入力」するのは少し難しいように思えるかもしれません。 以下の図は、織りパターンがどのように形成されるかを示しています。



スクリプトを書きましょう。 1次元配列array2を使用して、フレーム全体にスレッドを引き伸ばします。 1次元配列array1に、ペダルクランプのシーケンスを記述します。 array3（8x8バイナリアレイ）では、同時にペダルをクランプするペダルを記述します。

for(var i=0;i<length;i++){ for(var j=0;j<length;j++){ if(array3[array1[i]][array2[j]]){ context.fillRect(i, j, 1, 1); } } } 

スクリプト （Google Chromeで動作）。

即興織機の助けを借りて、さまざまなパターンを描くことができます。



しかし、歴史的に、平均的な人の足は2本以下です。 したがって、2つ以下のペダルを同時にクランプすると便利です。 織機の最も一般的なパターンの1つは次のとおりです。



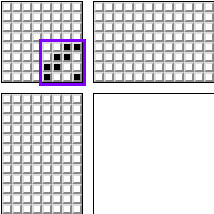
4フレーム。 そして、8フレームの変更：



突然、このテンプレートを使用して作成されたパターン（またはパターンのフラグメント）は、「ビリヤード」パターンに似ています。 さらに、これらのパターンは影付きです。



織機の「ビリヤード」パターンを選択する方法を学ぶことができます。 例：



記事の冒頭で、すでにこのパターンの断片を見ました。

織機で終了し、バイナリシーケンスを視覚化するスクリプトを記述します。 配列の1つを取り除くことができます-パターンは対角対称です。 残りの配列を埋める方法は？ 小学校：



シーケンスを取得します $$$\ sqrt {2}$。 配列を作成します。 配列のゼロ要素に、シーケンスのゼロビットを書き込みます。 シーケンスの各ビットを交互に取得します。 n番目のビットが1の場合-配列a [n] = a [n-1] +1に書き込みます。 ビット= 0の場合-[n] = a [n-1] -1を書き込む

$$

$$Q_n = \ lfloor n \ sqrt {x} \ rfloor \; （\ textrm {mod} \; 2）; \ quad n = 0,1,2、... \\ a_n = \ begin {cases} a_ {n-1} + 1、Q_n = 1; \\ a_ {n-1} -1、Q_n = 0 \ end {ケース}$$

  var a=[0]; for(var i=1;i<size;i++){ if(Math.floor(i*Math.sqrt(2))%2==1) a[i]=a[i-1]+1; else a[i]=a[i-1]-1; } 

私たちはチェックします：

  for(var i=0;i<size;i++){ context.fillRect(i, a[i]+50, 1, 1); } 

実際、私たちはすでに初歩的なフラクタルを受け取っていますが、継続します。

次に、マトリックスを扱います。



要約する $$$x$そして $$$y$。 モジュロを4で割ります。結果が0または1の場合-行列にtrueを書き込みます。 2と3については、falseを書きます。 マトリックスなしで実行できます（[n]が取る最大値と最小値が事前にわからない）。 [x]と[y]を要約します。 結果の量に、いくつかの数値を追加します $$$C$（金額が負の数である場合にそれらのケースを取り除くため）。 モジュロを4で除算します。値0および1の場合、座標でピクセルを塗りつぶします $$$x$そして $$$y$。

最終的なアルゴリズムは、数行しかかかりません。

  var a=[0]; for(var i=1;i<size;i++){ if(Math.floor(i*Math.sqrt(2))%2==1) a[i]=a[i-1]+1; else a[i]=a[i-1]-1; } for(var x=0;x<size;x++){ for(var y=0;y<size;y++){ q=(a[x]+a[y]+512)%4; if(q==0 || q==1) context.fillRect(x, y, 1, 1); } } 

フラクタルシーケンスを視覚化します。

$$

$$Q_n = \ lfloor n \ sqrt {2} \ rfloor \; （\ textrm {mod} \; 2）; \ quad n = 0,1,2、...$$

RGBイメージを取得するために、スクリプトを簡単に変更できます。

  q=(a[x]+a[y]+512)%4; /*if(q==0 || q==1) context.fillRect(x, y, 1, 1);*/ if(q==0) context.fillStyle = 'rgb(255,0,0)'; if(q==1) context.fillStyle = 'rgb(0,255,0)'; if(q==2) context.fillStyle = 'rgb(0,0,255)'; if(q==3) context.fillStyle = 'rgb(0,0,0)'; context.fillRect(x, y, 1, 1); 

上記では、合計a [x] + a [y]に数値を追加しました $$$C$。 この数を追加しない場合、合計の最小値= -8、最大値= 8（ $$$x$そして $$$y$0から750まで）。 削除する場合 $$$C$-場合によっては、合計が4番目の倍数ではなく負であることが判明し、これらの場合、ピクセルは塗りつぶされません（黒のまま）：

  q=(a[x]+a[y])%4; if(q==0 || q==1) context.fillRect(x, y, 1, 1); 

フラクタルの一部が架空の境界の下にあるかのように想像できます（この境界の下では、負の値のみが4番目の倍数である：-4、-8、-12、...）。

この境界がどこにあるかがわかります。

  if(a[x]+a[y]>=0) context.fillRect(x, y, 1, 1); 

モジュロを除算する代わりに、合計を特定の特定の値と比較して、フラクタルの1つの「レイヤー」のみをペイントできます。 例として、最小値と最大値の間の平均を取ります。

  q=(a[x]+a[y]); if(q==0) context.fillRect(x, y, 1, 1); 

値を最小から最大に変更すると、ダイナミクスの「レイヤー」がどのように変化するかがわかります。




さらに、「額」で[x]と[y]を比較し、フラクタルパターンを取得することもできます。

 if(a[x]==a[y]) context.fillRect(x, y, 1, 1); 

次のシーケンス：

$$

$$Q_n = \ lfloor n（\ sqrt {2} +1）\ rfloor \; （\ textrm {mod} \; 2）; \ quad n = 0,1,2、...$$

フラクタル：



RGB：



中間層：



ダイナミクス：

$$

$$Q_n = \ lfloor n \ sqrt {3} \ rfloor \; （\ textrm {mod} \; 2）; \ quad n = 0,1,2、...$$

フラクタル：



RGB：



中間層：



ダイナミクス：

$$

$$Q_n = \ lfloor n（\ sqrt {3} +1）\ rfloor \; （\ textrm {mod} \; 2）; \ quad n = 0,1,2、...$$

フラクタル：



RGB：



中間層：



ダイナミクス：

$$

$$Q_n = \ lfloor n \ sqrt {5} \ rfloor \; （\ textrm {mod} \; 2）; \ quad n = 0,1,2、...$$

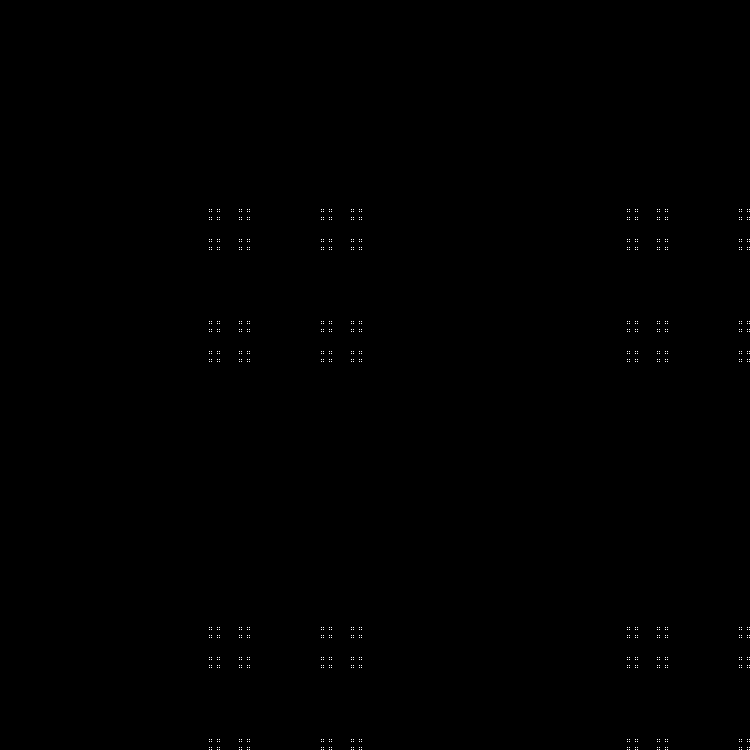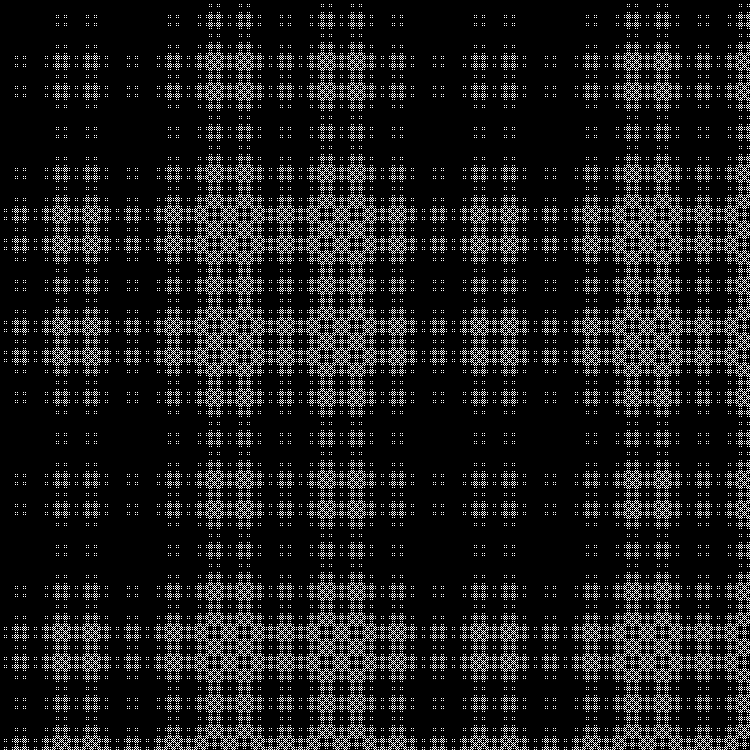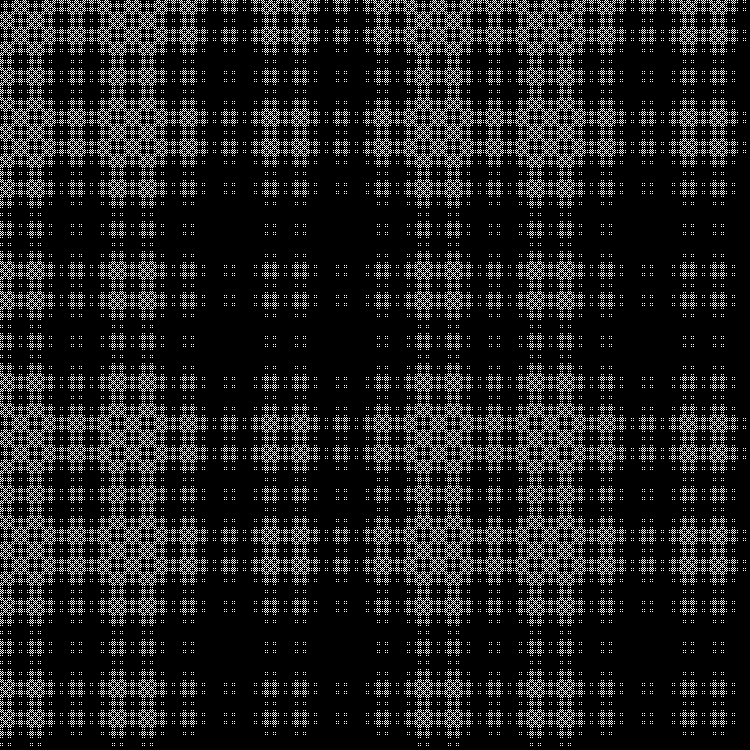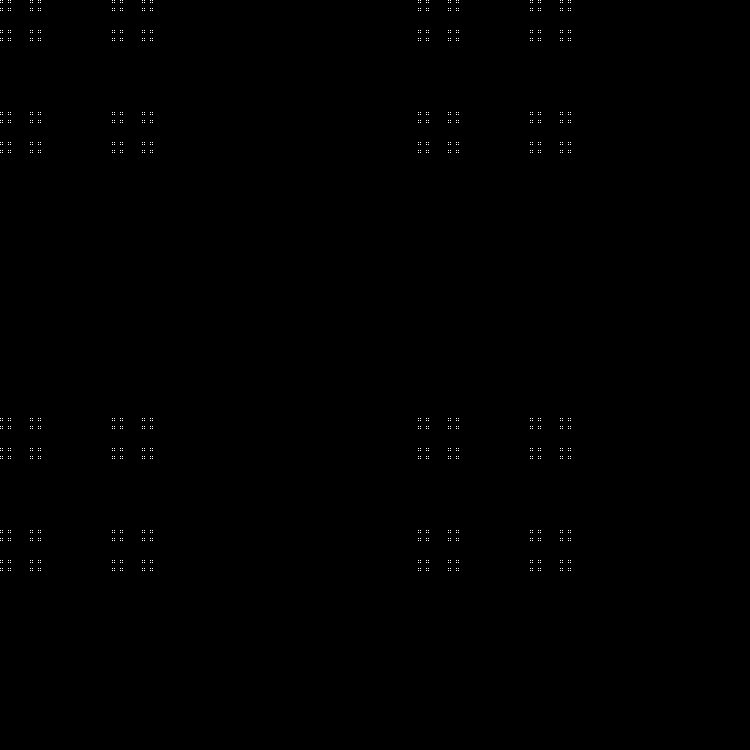
フラクタル：



RGB：



中間層：



ダイナミクス：



さて、私たちのお気に入りのフラクタル（このパターンの一部は、フィボナッチ数に等しいサイドサイズでビリヤードを使用して描画できます）：

$$

$$Q_n = \ lfloor n（\ sqrt {5} +1）\ rfloor \; （\ textrm {mod} \; 2）; \ quad n = 0,1,2、...$$

フラクタル：



RGB：



中間層：



ダイナミクス：



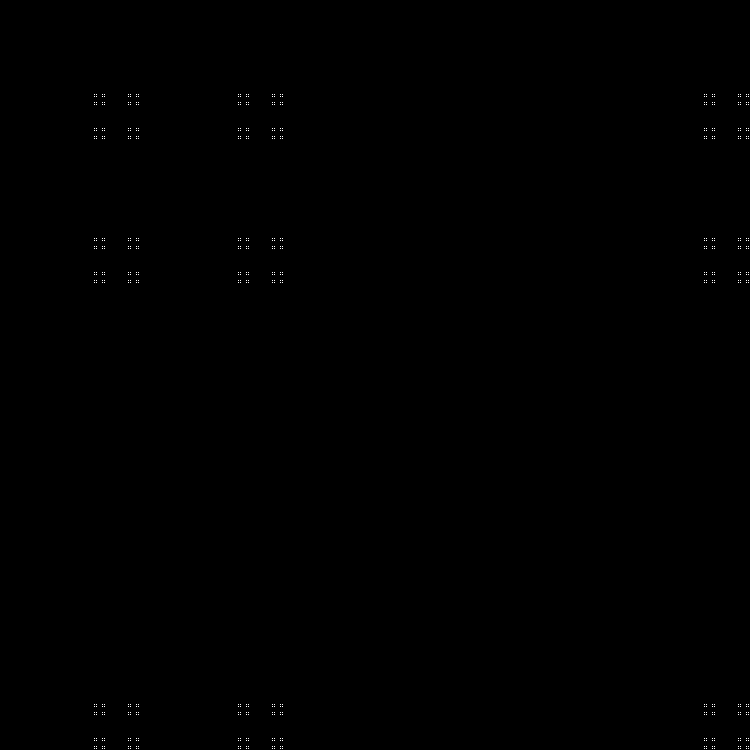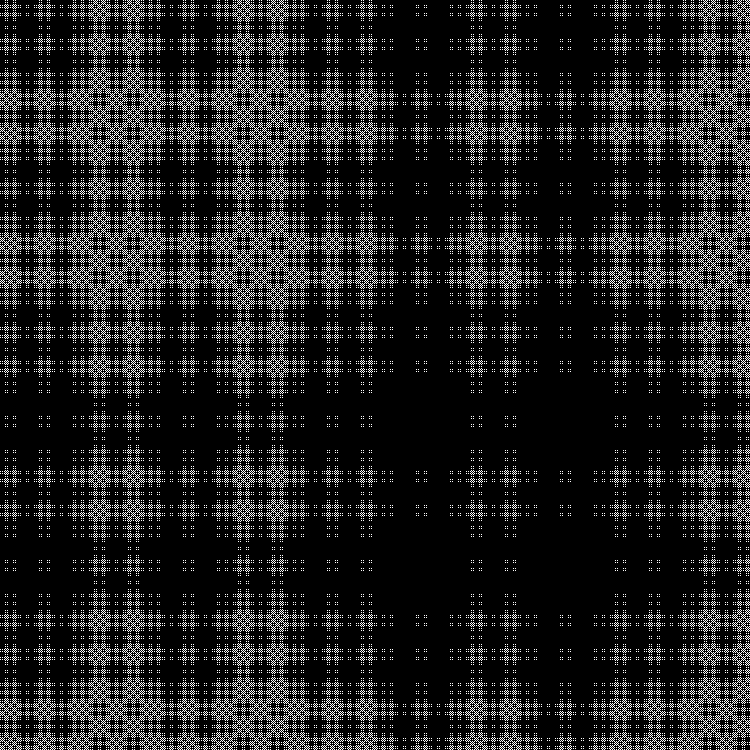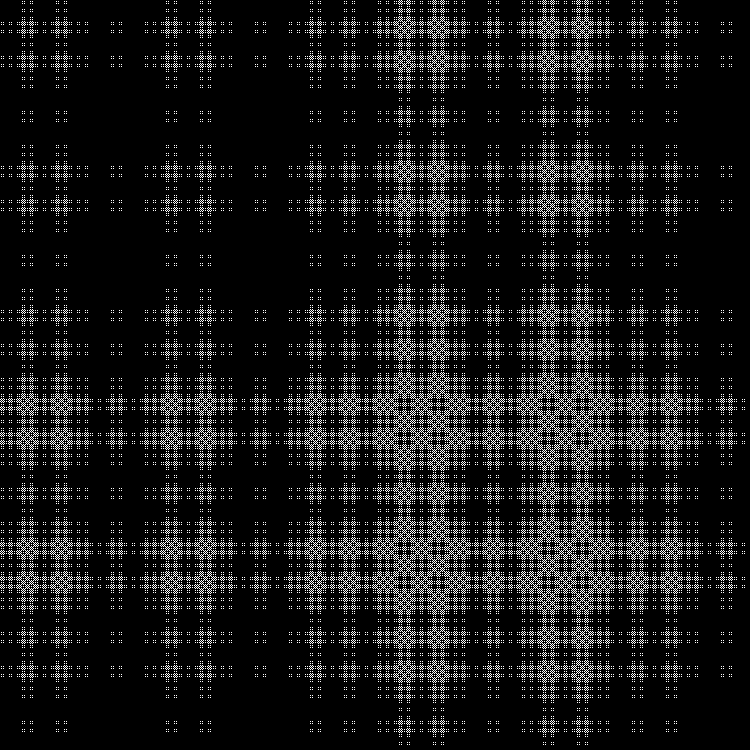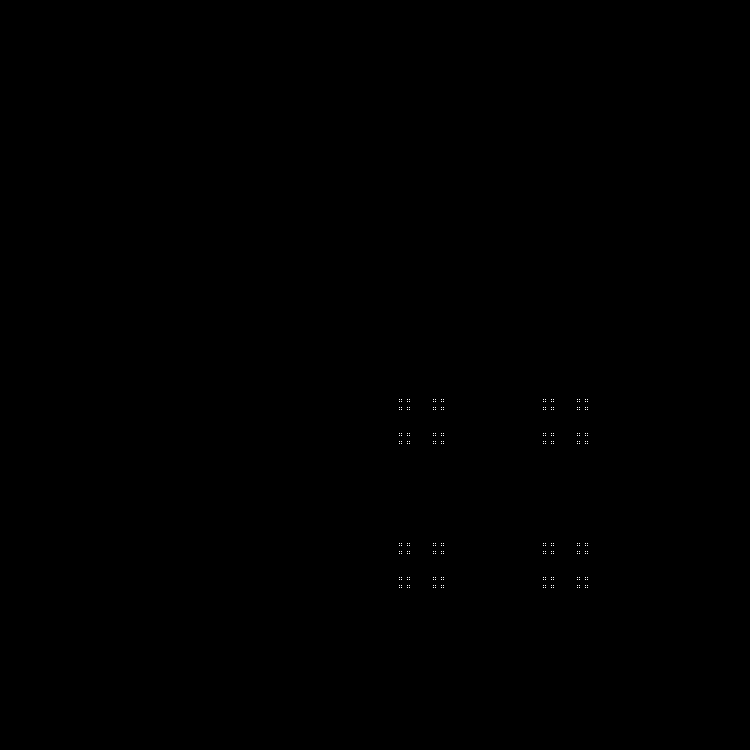
完了する別のシーケンス：

$$

$$Q_n = \ lfloor n ^ {2} \ sqrt {2} \ rfloor \; （\ textrm {mod} \; 2）; \ quad n = 0,1,2、...$$

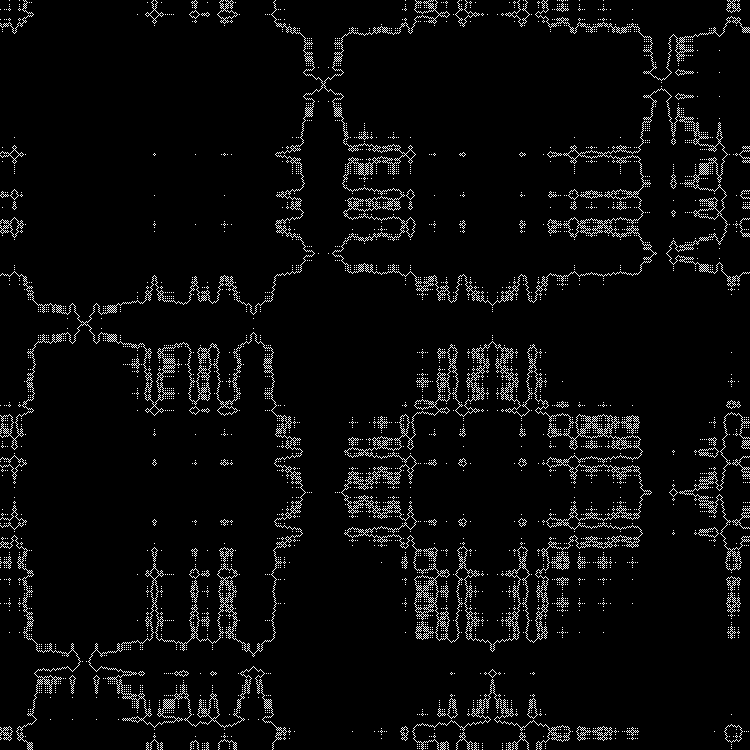
パターン：



RGB：



中間層：



ダイナミクス：



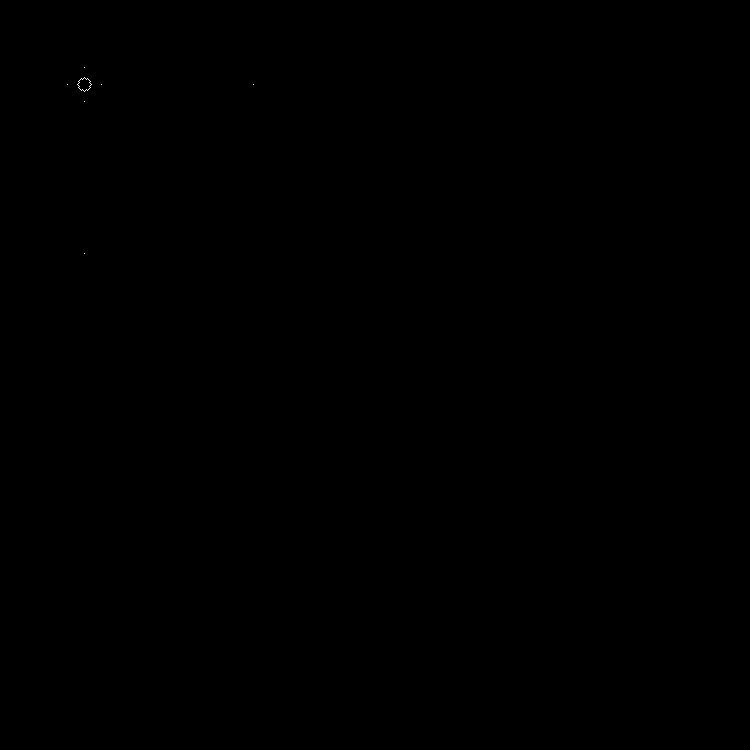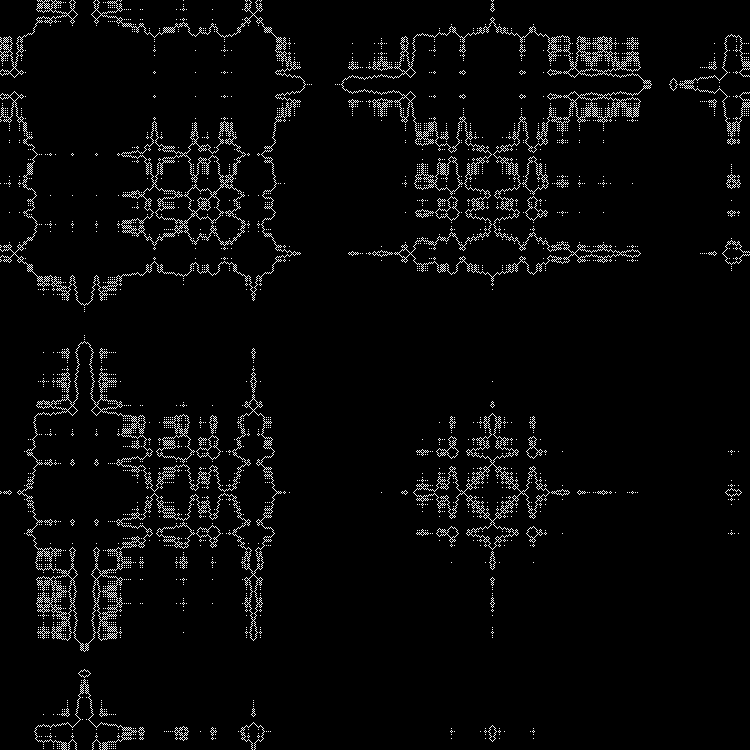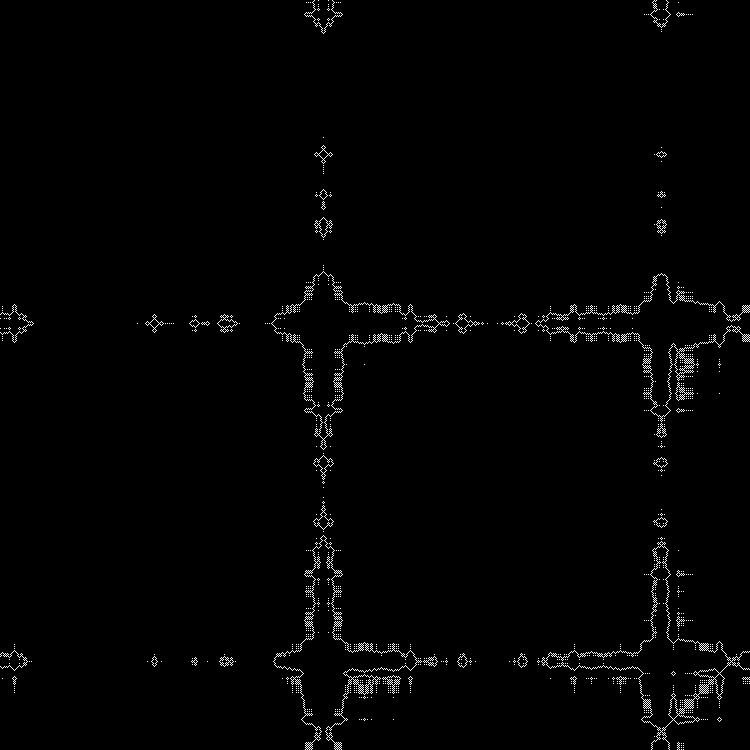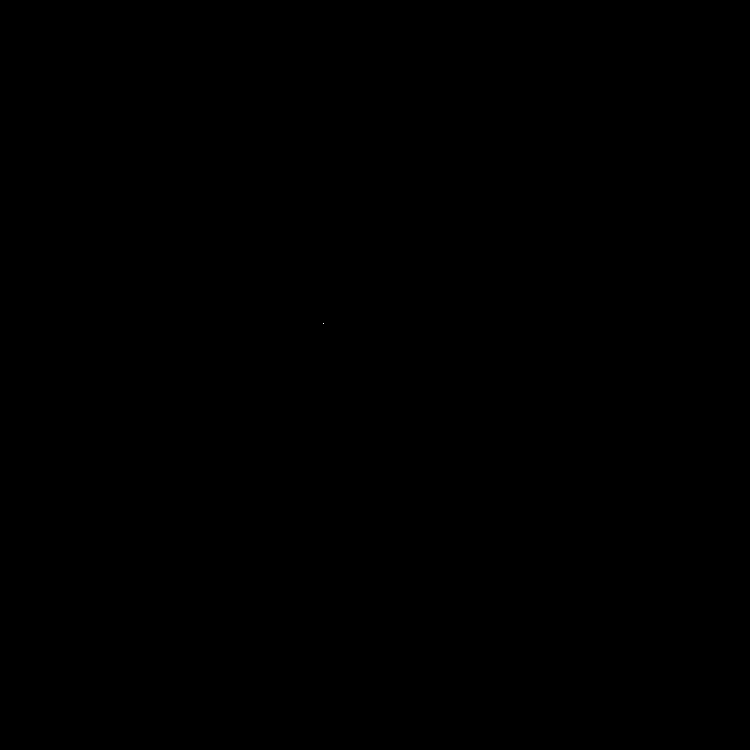
他の平方根をスクリプトに組み込むことができます 。 （小数値で駆動できます）。

2番目のスクリプトでは、シーケンスを手動で駆動できます。

ビリヤード用の別のスクリプト 。 マウス座標-ビリヤード寸法。 左側のパターンは、除算の残りを使用して取得したシーケンスから形成されます（詳細は前の記事を参照）。 右側-パリティ $$$\ lfloor n \ frac {y} {x} \ rfloor$。