はじめに

プロジェクトについて

プロジェクト「絶対為替レート」は、ペアの為替レートの分析、それらからの絶対為替レートの配分、およびそれらの分析に従事しています。 プロジェクトの枠組みの中で、ペアレートから絶対為替レートに変換する方法論が得られました。 このために、絶対通貨ABSが定義されています。 すべての通貨はABSに関連して引用されます。

この技術の詳細な説明は、 「通貨ペアから絶対為替レートへ」という記事に記載されています 。

問題について

この記事では、為替レートの一貫性の定性分析の問題に取り組んでいます。
通貨間の関係を調べる必要があるのは、投資ポートフォリオ内の金融商品の選択の要件と、通貨に関連する他の通貨のデータに基づいて通貨の行動を予測する能力によるものです。

投資ポートフォリオに多方向接続性の高い機器を含めることをお勧めします。 これにより、ポートフォリオの全体的なリスクを軽減できます。

また、高度な接続性を持つツールを見つけた場合、一部の動作に基づいて、他の動作を予測できます。

実験について

メソッド選択

実験の初期データとして、絶対為替レートのデータ系列があります（ ソースファイルの「絶対為替レート」シートを参照）。



一連の数値データの接続性を調べるには、ピアソン相関を使用するのが最適です（ 相関-Wikipediaを参照）。

相関係数の値の範囲は「-1」から「+1」です。 大きな負の値は、強い多方向の関係を示します。 大きな正の値は、強い単方向接続を示します。 係数が「0」に近いことは、通信がないことを示します。

何を得たいですか？

この実験の目的は、高いつながりのある通貨のグループを取得することです。 さらに、コミュニケーションの兆候にも関心があります。

会場

すべての計算はWolfram Mathematicaシステムで実行されます（ Wolfram Mathematica-Wikipediaを参照）。 そして、 Wolfram.Cloudの無料クラウドリソースを使用します。

指定されたリソースを使用すると、計算付きのオンラインノートブックを作成したり、一般的な表示用のアクセスを提供したりできます。 この実験のノートはここにあります 。

計画

以下の計画に従って計算を行います。

最初に、相関行列を計算します。 マトリックスの列と行は個々の通貨に対応します。 列と行の交点に、ペア相関係数があります。

次に、最も強いつながりを持つ通貨のペアを選択します。 選択したペアをグラフに配置します（ グラフ（数学）-ウィキペディアを参照 ）。

グラフのノードは通貨です。 グラフの端は、通貨間の関係を示します。 リブの色は、コミュニケーションの兆候を示します。 緑は正の関係を示し、赤は負の関係を示します。

指定された一連の計算は、絶対コースとその変更の両方で実行されます。 絶対コースの関係の分析により、遅いプロセス（1日以上）を探索できます。 絶対為替レートの変化間の関係を分析することで、通貨間の高速接続（1日）を調べることができます。

結果

サンプリング深度

ソースファイルには、過去150日間のデータが含まれています。 彼らによると、計算が行われます。

通貨クラウド

実験には45の通貨が含まれていました。



通貨の完全なリストは、ソースファイルの「通貨の概要」シートで確認できます 。

絶対レート相関

上記（計画を参照）では、絶対レートの相関行列を計算することが計画されました。 結果を下の図に示します。



ここで、赤は正の接続に対応し、青は負の接続に対応します。 理解のために、グラデーションスケールが与えられています。 下と左は通貨ティッカー（短い名前）です。

絶対レート依存グラフ

相関マトリックスにより、通貨の2つのグループを高いつながりで区別することができました。 これを行うために、0.9より高い相関を持つペアが選択され、グラフに転送されました。



最初のグループは、米ドルに高度に依存する通貨を集めました。 これは、石油、香港ドル、米ドル自体で取引されているアラブ4か国の通貨です。 すべての依存関係は正（単方向）です。

2番目のグループはヨーロッパの通貨を集めました。 中央にはユーロそのものがあり、その周りにはポーランド、ルーマニア、デンマークの通貨があります。 すべての依存関係は正（単方向）です。

絶対レートの相対的な変化

さらなる研究のために、絶対レートの相対的変化のシリーズを計算しました。 計算式は次のとおりです。



連続する値の差は、2つのうちの早い方に相関します。 したがって、絶対レートの相対的な変化を受け取ります。

絶対レートの相対的な変化の相関

絶対コースについては、絶対コースの相対測定の相関行列を取得します。 マトリックスをグラフィカルに表示します。



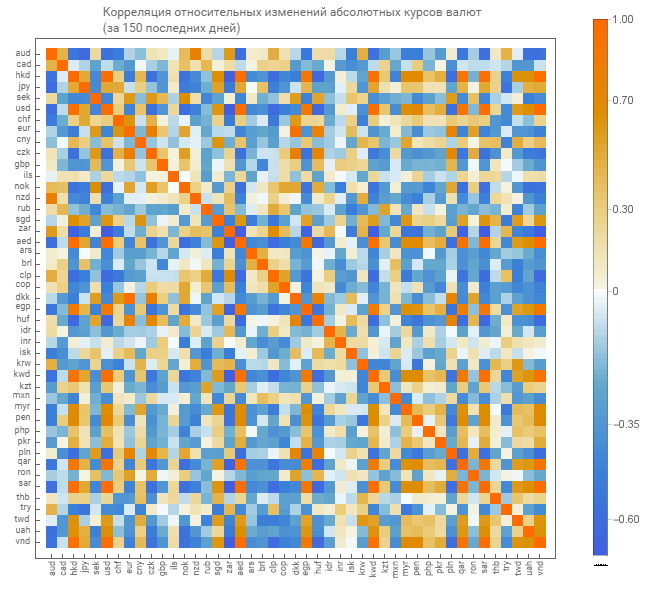
すでに明るいトーンのマトリックスがあります。 これは、つながりの度合いが低いことを示しています。

絶対レートの相対的変化の依存グラフ

相対的な変化の相関行列から、連結性の高い通貨のペアを選択します。 ここでのサンプリングレベルのみがすでに0.6です（ここおよび上記では、この係数は、グラフへの出力用の少数のペアを考慮して選択されています）。



相対的な変化の場合、通貨の3つのグループを受け取りました。 上のグループは、オーストラリアとニュージーランドの通貨を組み合わせました。 低いグループはヨーロッパの通貨を集めました。 香港ドル周辺の中央のグループは、米国、ベトナム、アラブの5か国（石油輸出国、南アフリカ、ペルー）の通貨を組み合わせました。

さらに、南アフリカランドへの高い負の依存性には興味深い特徴があります。

結論

実験の結果、次のようになりました。

相関行列データを数学的グラフに入れることは、相関行列の視覚化に適しています。 この方法をさらに適用すると、一連の数列の関係の理解が簡単になります。

通貨市場をクラスタリングするための正式な方法が見つかりました。 ヨーロッパ、アメリカ、アジア、オセアニアの市場を正式に区別することができました。 この方法は、さまざまな国の市場間の相互影響を明らかにするための経路を大幅に短縮し、金融アナリストにとって優れたツールとなります。

南アフリカのランドを米ドルとともに投資ポートフォリオに含めることにより、そのようなポートフォリオのリスクが軽減されます。

記事のカタログ