高速フーリエ変換（FFT）に基づく定常ランダムプロセスのスペクトル推定の方法はよく知られており、工学の実践で広く使用されています。 それらの欠点には、特に、プロセスの観測間隔が十分に長くない推定値の高分散（低精度）が含まれます。これは通常、パワースペクトル密度（PSD）の強力な「インデント」グラフに現れます。 スペクトル推定の代替方法の1つは、以下の例で考慮される自己回帰法であり、工学の実践ではあまり知られていません。 多くの場合、この方法により、PSD（図1）のはるかに優れた推定値を取得することが比較的容易になり、調査中のランダムプロセスに関するより深い情報を取得することもできます。
図1「短い」プロセスPSDの古典的および自己回帰評価デモンストレーションのために、離散時間信号（シーケンス）x [i]が合成されました。 信号は、機械システムの特性をシミュレートするARMAモデル（デジタルフィルター）を使用してモデル化されます（1）-パラメーターm = 1 kg、c = 100 N / m、k = 2の「単一質量」オシレーターで質点x（t）を移動5 kg / s、および力摂動による-1 N
2の分散、時間サンプリング間隔Δt= 0.12 sのガウス「ホワイト」（離散化を考慮）ノイズf（t）。
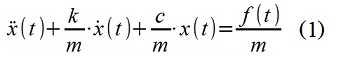
モデル作成（2）。 モデルを構築する方法はすでに
ここで以前に考えられまし
た 。
x [i]-0.6388・x [i-1] + 0.7408・x [i-2] = 0.009667・f [i-1] （2）
（2）を使用して、5万サンプルのシーケンスが合成され、そのために、よく知られたソフトウェア環境の正規分布ランダム変数randn（）のジェネレーターが使用されました。
プロセスx [i]のシミュレーションが完了した後、モデル（2）の定量的パラメーターは不明であると見なされます-プロセス自体と、ある程度まで、最も一般的な用語でのモデルの特性に関する情報が研究に利用可能です。
ウェルチ法を使用して、50,000点シーケンスのスペクトル推定を実行し、セグメントサイズを256サンプルに等しくし、ハミングウィンドウとセグメントの60％のオーバーラップを適用しました。 このような推定の標準偏差は、シーケンスの長さが約200の非重複セグメントであるという事実に基づいて、おおよそ7％と概算できます。
さらに、実験の実際の条件下では、はるかに短いシーケンスが研究に利用可能であると想定し、この信号の最初の500個のサンプルのみで研究が行われました。
推定値は、同じパラメーターを使用してウェルチ法によって取得されます。 このような推定値の標準偏差は〜70％であり、グラフの非常に強い「堅牢性」が顕著です（図2）。
図2.古典的方法による「長い」および「短い」プロセスのPSDの評価SPMプロセスの関数（グラフ）のおおよその形式を知っているという事実に基づいて（たとえば、プロセスの既知の物理的性質-ホワイトノイズのもとでの単一質量発振器、またはより長い実装が利用可能な同様のプロセスの評価から）、 2次自己回帰モデルを使用（AR（2）、または= ARMA（2.0））。
モデルの順序を決定することは非常に重要なポイントであり、順序のエラーは推定結果の非常に大きなエラーにつながる可能性があります。 ここではまだ検討されていないメソッドがあり、分析されているプロセスのみに基づいてモデルの順序を決定するのに役立ちます。
モデルパラメータの推定は、自己回帰プロセスの有名なユールウォーカー方程式を使用して実行されました（スクリプト構造をわずかに単純化するために少し変更されています）。
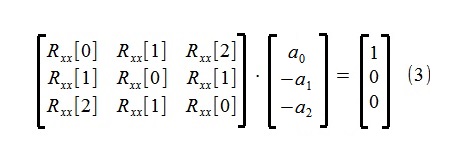
式からわかるように、パラメーターを決定するために、自己回帰シーケンスRxx [0]、Rxx [1]、Rxx [2]の最初の3つのメンバーのみが使用されます。これらは、初期500点シーケンスx [i]からコレログラム法によって推定されました〜4.5％。
（ちなみに、a
1 、a2
2などの前の「cons」は非常に不便であることは明らかです。以前の「エンジニアリング」ソースでは、経済におけるARMAモデルの圧倒的な「予測」使用のために登場しましたいいえ。AR係数のこのような理解をここで使用する必要があることはすでに疑っています。
（3）の相関行列は、実際には常に厳密な対角線の有病率を持っています。 Rxx [0] | > | Rxx [i] |観測ノイズの存在によるものも含み、その結果、取り扱いに問題はありません（解決策を見つける（3））。
（統計シミュレーション誤差の大きさの問題を明確にするために、たとえば、50,000サンプルから得られたコレログラムの分散推定値と比較して、500サンプルから得られた推定値Rxx [0] = 2.2606e-04 m
2 = 2.4238e-04 m
2 50,000サンプルのウェルチ法で得られたPSD面積の被積分関数による推定（図2）= 2.4232e-04 m
2 ）
見つかった推定値Rxx [i]を代入すると、次のようになります。
次のモデルパラメーターは、
0 = 11325.9と決定されます。 a
1 = 7090.1; a
2 = -8411.5; （3）からわかるように、ここでは仮想着信白色雑音の分散を= 1に設定し、その代わりにゲイン係数a
0を決定しました。 PSDの自己回帰推定は、一連の係数a
0 、a
1 、a
2のフーリエ変換によって構築されます。
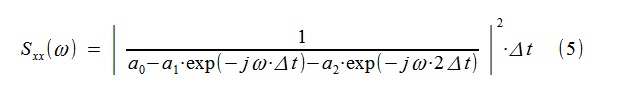
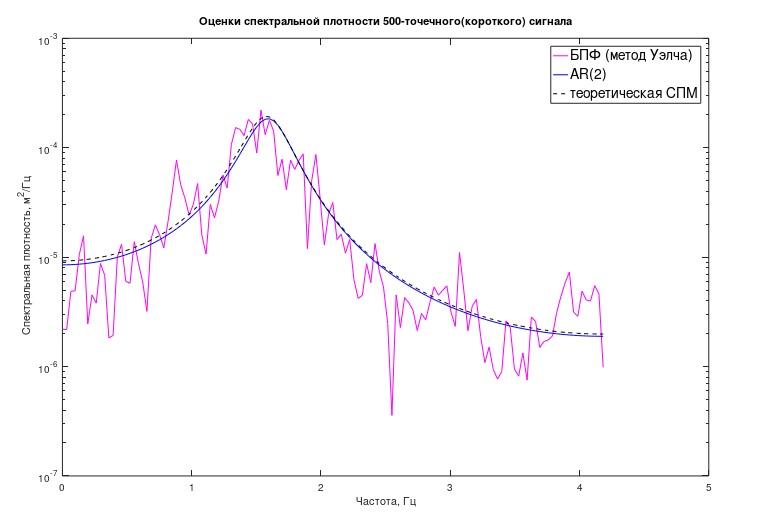図3「短い」プロセスPSDの古典的および自己回帰評価同様に、（5）に類似した式によると、PSDの「理論的」スケジュールも事前に構築され、もちろんそこのモデル係数のみが異なります（（2）とは異なります）。
グラフは、PSDのAR評価が理論的に予想されるものに非常に近いことが判明したことを示しています。 グラフに加えて、プロセスおよび関連する機械システムの分析特性を評価することもできます。 この場合、これらはモデルの「極」であり、モデルの「共鳴」ピークの周波数と関連する「品質係数」を数値的に特徴付けます。
（5）から、ラプラス変換を使用してモデルの伝達関数の不連続性を検索するための関係を見つけます（jωをλ=-ε+jωで置き換えます）。
得られたARモデルについて、λ1,2 = -1.5427±j・10.1514がこの方法で計算されました。これは、プロセスの生成に使用された元のモデルに非常に近いものです。
λ1.2theor = -1.2500±j・9.9216（つまり、それぞれ共鳴ピークの位置、1.615 Hz（理論上）および1.579 Hz（決定済み））。
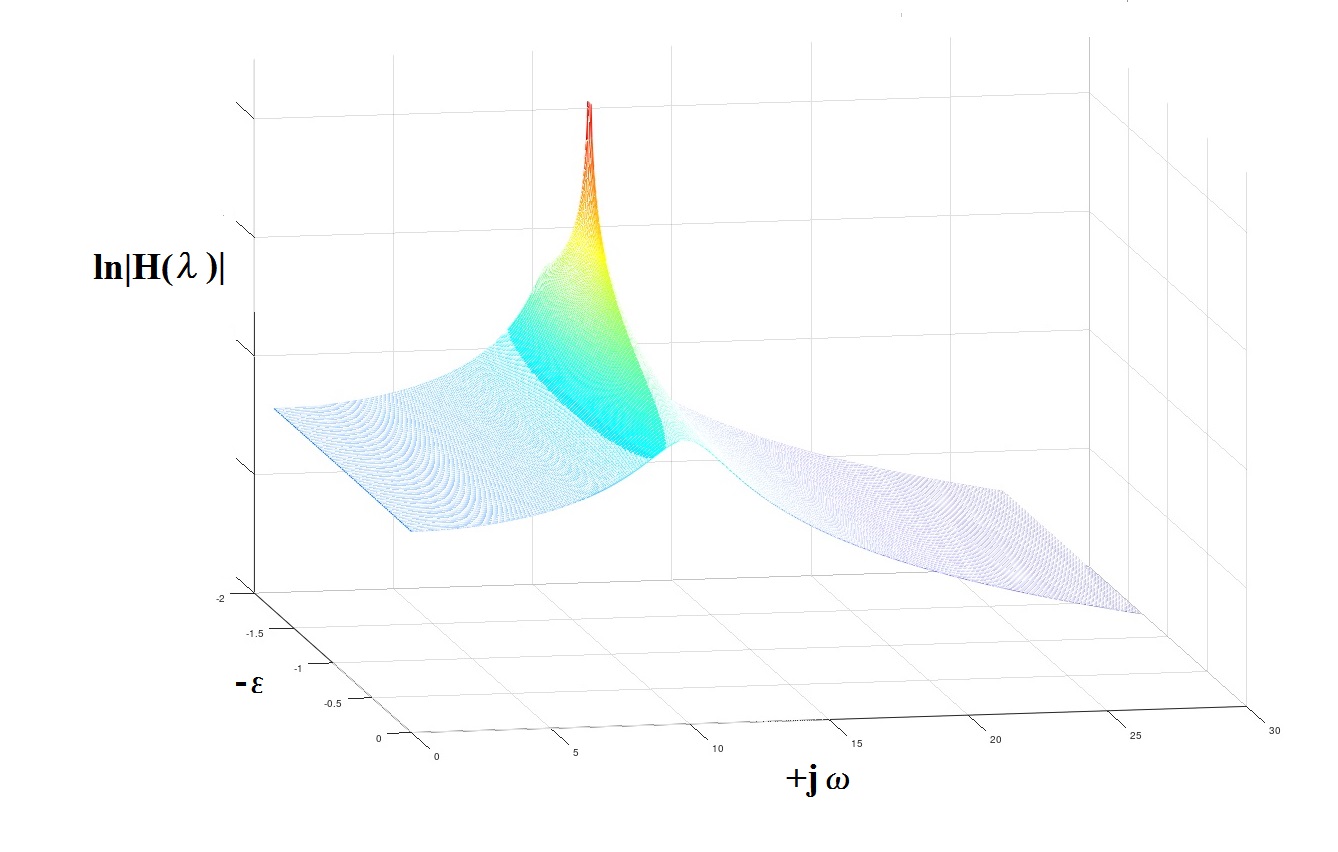図4「極」の概念について結論にいくつかのコメントと推奨事項。
- ARモデルの「過剰な」（大きすぎる）次数は、総誤差のあるPSD推定値を取得するリスクの観点から、通常、不十分であるよりもはるかに危険性が低くなります。
- 原則として、ARモデリングにより、共振周波数jωkをかなり正確に決定し、対応する「ピーク」-εkの幅をあまり正確に決定することはできません。
- ARMA-多くの情報源によると、モデルはARモデルよりもはるかに小さい次数（サイズ）になることがあり、モデルの精度を向上させることを目的としているようです。 ただし、モデルのMA部分を評価することははるかに難しく、一般に、MA部分にさらに変換するために、高次ARモデルを取得する最初のステップを含めることができます。 これらのソースに関連して、高次ではあるがスペクトル推定に正確にARモデルを使用することの推奨可能性について、別の意見も表明されています。
- 非常に短い場合、および非定常プロセスの場合、自己相関関数の推定行列の代わりに、通常、共分散行列が（3）で使用されます。
- 自己回帰スペクトル推定の問題の詳細な研究については、S.L。 マープルml。 「デジタルスペクトル分析とその応用」、M。、ミール、1990