ピークの近接について

「これを理解する前は、奇跡のようです。 しかし、その後は特別なことは何もありません。」

いいえ、山についてではなく、数についてです。 数学では、定式化は誰でもアクセスできる質問がありますが、解決策は簡単ではなく、特別な準備なしでは説明が困難です。 これらの問題の1つは、次のように簡単に表現できます。有向グラフで距離を正しく計算する方法は？ このやや抽象的な問題は、非常に具体的な動機付けタスクに還元できます。 1つの写真に収まります。

1.問題の声明。 私は一方に住んでいますが、もう一方には住んでいます。

小さな町は（たとえば、川によって、ピークのコンテキストでは渓谷の方が適していますが）2つの地区（部分）に分割されます。 $$$A$そして $$$B$。 地区間の通信は、2つの車線がある単一の道路（橋）に沿って行われます。 $$$A$に $$$B$その逆も同様です。 人口増加に関連して、道路の容量を増やすという疑問が生じました。 いつものようにお金はかろうじて十分であり、一方向の1車線にのみ十分です。 1つの車線で地域を近づけることは明らかですが、問題は-どのくらい正確ですか？ あなたは都市の狂った数学者であり、 合理的な答えを得るために招待されたのはあなたでした。

一方向に別のストリップを構築する場合、エリアはどれくらい近くにありますか？

高度な表現

Konigsbergブリッジの代わりに、もう少し厳密なグラフ理論言語を使用できます。 そのため、2つの頂点（ノード）を持つ有向グラフがあります $$$A$そして $$$B$。 順方向と逆方向の接続の大きさ（導電率、帯域幅）は、最初は同じです。 問題は、いずれかの方向の導電率が2倍になった場合、ノード間の距離がどれだけ変化するかです。

そして、はい、もしあなたが本当の数学者の溶接工なら、直接値とフィードバック値の解決策を提供（そして正当化）できます。 理想的には、任意の数のノードとリンクを持つグラフの場合。

親密さと酔っ払いの放浪

リージョン間の通常の距離（キロメートル）は、道路の有無に依存しないことは明らかです。 したがって、ここには収まりません。通信に依存する必要があります。 より多くの地区が接続されている-それらがより近い-より多くの住民が時間単位で別のエリアに到達できます。

無向グラフのノード間の近接性の尺度を評価するために、いわゆる抵抗距離を使用できます。 以前、この距離の特性については、 いくつかの記事で既に説明しています。

電気ネットワークに関して言えば、抵抗距離は実効抵抗の概念と同等です。 したがって、電子言語では、問題は次のように定式化できます。 2つのノードの間には、同じ導電率の2つのダイオードが反対方向に含まれています。 別のダイオードを追加すると、これらのポイント間の抵抗はどのように変化しますか？ （電気言語が失敗し、ここでナンセンスを書いた場合、私は謝罪します）。

また、 酔っ払いのランダムウォークの確率について、マルコフ言語で効果的な抵抗を解釈できます（トピック「Googleのランダムウォークと電気ネットワーク」を詳しく調べたい人向け）。

抵抗距離は2次で、線形距離の2乗に対応します。 二次距離は、二次とも呼ばれます 。 ただし、この問題では他の（線形）距離は使用されないため、ここではquadransという用語は必要ありません。 （それがなくても鳥の舌は十分です）。

一般に、「抵抗距離」という用語も見栄えがよくありません。 彼は、私たちが科学にとって未知の異常な距離について話していることを暗示しています。 実際、抵抗距離は通常のユークリッド距離です。 しかし、アフィン空間では。 この機能をさらに使用します。

実際、問題は何ですか？

「抵抗距離」が何であるかを知っている場合、与えられたグラフに対して「それだけを取り、計算する」ことができないのはなぜですか？

うん 原則として、簡単です。 無向グラフについて話している場合。 市が両方向にストリップを構築した場合、抵抗距離はちょうど半分に減少したでしょう。 抵抗は導電率に反比例するため、導電率（帯域幅）は2倍になります。 そして、各方向に2つのバンドを追加した場合、距離は3倍減少します。 ここではすべてが非常に簡単です。 （そしておそらく、ここの誰かがすでに解決策の一般的な形を推測できるでしょう。そしてさらに先へ進みます）。

対立する関係が等しくない場合、すべてが複雑になります。 そして非常に厳しく。

有向グラフのピークの近接度（抵抗距離）を決定するための、一般的に受け入れられている簡単な法的方法はありません。

（これは私の論文です-たぶん誰かが私を説得することができます）。 「いいえ」-これは、教科書、ウィキ、および頭の中にないことを意味します（より正確には、さまざまな仮定と定義を必要とするさまざまな著者のさまざまな方法があります）。 方法があります（それほど単純ではありません）。 この記事では、それについて説明しています。

有向グラフが存在する場合の距離の定義は、有向グラフについて説明する場合に明確にする必要があります（非可換メトリック、謝罪します）。 距離について話すことができます $$$A$前に $$$B$、しかしからできます $$$B$前に $$$A$。 そして、これらの距離は常に等しいとは限りません。 問題ではどのような距離について話しているのでしょうか？

ユークリッド距離規則

私たちは現れ、深呼吸します。 抵抗距離は通常のユークリッドであると既に述べました。 これは、その定義を2つの要素の差のノルムとしてのユークリッド距離の定義に縮小できることを意味します。

$$$S（A、B）= | A-B | ^ 2 =（A-B）^ 2 =（A-B）\ cdot（A-B）= S（B、A）\ quad（1）$

この定義は、要素の順序に依存しません-これは、要素の可換距離、近接度（より正確には距離）です。 式内のポイントは、スカラー積演算（メトリック空間）を意味します。 したがって、式（1）を開示できます。

$$$S（A、B）= S（B、A）= A ^ 2 + B ^ 2-A \ cdot B-B \ cdot A \ quad（2）$

ここに $$$A ^ 2 = A \ cdot A$、 $$$B ^ 2 = B \ cdot B$-要素の規範。 グラフに関しては、通常、要素のノルムはゼロです。 元の問題では、ノルムについては何も言われていないので、それらをゼロにすることができます（アフィン空間の要素のノルムの意味についてはこちら 。さらに詳細はこちら ）。 次に、目的の距離の式は次の形式を取ります。

$$$S（A、B）=-（A \ cdot B + B \ cdot A）= s_ {AB} + s_ {BA} \ quad（3）$

式（3）によると、問題を解決するために必要なのは、有向グラフ内の要素（ノード）のスカラー積を見つけることだけです（言うのは簡単ですが、これを行う方法は？）。

途中で、式（3）は、要素間の近接性の一般的な（可換）尺度を示しています $$$A$そして $$$B$2つの有向距離の合計です。

$$$s_ {AB} =-A \ cdot B$-からの方向距離 $$$A$前に $$$B$、
$$$s_ {BA} =-B \ cdot A$-からの方向距離 $$$B$前に $$$A$。

2.決定。 砂丘の長い道のり

ランブルはおさまった。 楽しみは終わりました。 次に、有向グラフのノード間のスカラー積を計算する方法の本質の説明の鈍い詳細があります。 これは「指で簡単に」と言う方法がわからない部分です。 しかし、この記事で最も重要なのはここです。 時間を浪費する価値のあるもの。

推論の一般的な行は次のとおりです。 新しい追加の仮定の感情なしに、対称空間のメトリックの既知の特性を非対称空間に慎重に転送します。 必要なのは、アフィン空間でのメトリックの特性を考慮することです。

接続されたグラフは（有向かどうかに関係なく）アフィンメトリック空間を定義します。 対称（可換）実行におけるそのようなスペースのいくつかの特性は、すでに述べた一連の記事で、またはより正確かつ詳細に言及したlongridで （カオス的に）記述されました。 急いで切り替えないでください-以下では、（舌のねじれで）メインのスクイーズを与えます。

アフィンメトリック空間（無向グラフ）

何が重要ですか。 最初によく知られています。

1.空間の親和性とは、空間のベクトルと要素の概念が異なることを意味します。 ベクトルは要素の違いです。 この一見取るに足りない機能は、メトリックが空間で定義されている場合、重大な結果につながります。

2.スペースは、要素で構成される基底によって定義されます。 グラフの頂点はスペースの基礎です。 グラフ内の関係により、そのメトリックプロパティが決まります。

3.グラフの接続特性は、 隣接行列です。 しかし、メトリック（およびその他の）プロパティの場合、グラフのラプラシアン（キルヒホッフ行列）がより重要です。 $$$L$。

4.グラフのラプラシアンは、ほぼ計量テンソルです。 「ほぼ」-ここでは、不完全であることを意味します。 ラプラシアンは縮退行列であるため、可逆的ではありません。 そして、標準の計量テンソルは完全に可逆です。

今ではあまり知られていない。

5.メトリックアフィン空間の要素とベクトルの違いにより、その中にヌルベクトルが存在します。 $$$\ mathbb z$。 可換（対称）空間におけるヌルベクトルを持つ要素のスカラー積は、ユニティに等しくなります（非可換空間では、乗算の方向に依存します）。 ゼロベクトルがないと、グラフ空間は完全ではありません！ これは重要です。

6.基底の直交中心は 、ヌルベクトルに関して双対です。 $$$Z$。 これは、基底の他のすべての要素（ゼロベクトルを除く）に直交する要素です。 要素の直交性は、それらのスカラー積がゼロであることを意味することを思い出してください。 三角形のオルソセンターは外接円です。 はい、完全なアフィン空間では、非ゼロのノルムを持つ要素は点ではなく、n次元の球体です。

7.グラフのラプラシアンと直交中心の座標が完全になります（本格的な計量テンソル）。 言い換えれば、完全なラプラシアン $$$Lm$通常のグラフラプラシアンです $$$L$しかし、直交中心の重心座標によって境界が定められています。

8.完全なラプラシアンの反転により、完全なグラミアンを取得できます。 $$$Gm$-基底の要素のスカラー積の行列（この場合、グラフの頂点）。 このグラミアンは、本格的な空間の計量テンソルでもあります。

9.フルグラミアンのフレーミングは、ユニットのタプル（基底要素とゼロベクトルのスカラー積）です。 コーナー-ゼロでは、これはゼロベクトル自体のノルムです。
有名なCayley-Menger行列はほぼ規則的なグラミアンです。

その結果、請求項8に従って、グラフのノード間のスカラー積（および、したがって距離）を決定する問題は、基底の初期メトリックテンソルを決定することに帰着すると結論付けます。 $$$Gm$。

グラフの完全なグラミアンを構築する方法が必要です $$$Gm$与えられた（不完全な）ラプラシアンについて $$$L$。

対称結合の場合、ラプラシアンからの完全なグラミアンの構築（およびその逆）は、特定の困難を引き起こしません。 この場合、基底の要素とゼロベクトルのスカラー積は可換です-乗算の順序に依存しません：

$$$\ mathbb z \ cdot A = A \ cdot \ mathbb z = 1$

有向グラフ（非可換空間）の場合、問題は複雑です。 有向グラフの可能な接続の数が2倍になるためだけです。

非可換アフィン空間（有向グラフ）

有向グラフのラプラシアンの性質については、ハブにも書きました ラプラシアンのポテンシャルを使用してオブジェクトをランク付けする方法を教えてくれました。 基底に関しては、ラプラシアンのポテンシャルはゼロベクトル（ラプラシアンの消滅）の二重座標です。

この記事では、メトリックプロパティに興味があります。 グラフが有向の場合、頂点間のスカラー積は次数に依存します。

$$$A \ cdot B \ ne B \ cdot A$

これは、有向グラフの二重座標が（左右に）分割されることを意味します。 ヌルベクトルのスカラー積と基底の要素（グラミアンの境界）の値も、因子の順序に依存します。 したがって、可換空間とは対照的に、ここではゼロベクトルの二重座標の半分は不明であり、決定する必要があります。

$$$\ mathbb z \ cdot A \ ne A \ cdot \ mathbb z$

ただし、既知の数量は多数あります。

まず、ラプラシアン自身が知られています。 さらに、行の合計がゼロであることが知られています（一般的な場合、これはオプションの要件ですが、有向グラフのラプラシアンでは通常これが当てはまります）。 また、要素の重心座標は空間メトリックスから独立しているため、一意であることも重要です。 つまり、グラフのラプラシアンの境界は、有向グラフと無向グラフの両方で対称です（この点はすぐにはわかりませんでした）。 最後に、基底の要素のノルムがわかります（通常、グラフではゼロに等しい）。

ラプラシアンとグラミアンをつなぐアイデンティティにおいて、すべての既知および未知のものを代用することが残っています。

$$$Lm \ Gm = I$

ここに $$$I$単位行列です。 このアイデンティティにおいて、不完全なラプラシアンから完全なラプラシアンへの移行の意味。

黙って信じて

言葉から行為に移りましょう。 これはラプラシアンがどのように見えるかです $$$L$2つのノードのグラフの場合：

$$$L = \ begin {bmatrix} c_1＆-c_1 \\ c_2＆-c_2 \ end {bmatrix}$

簡単にするために、接続を番号で指定しました。 $$$c_1 = c_ {AB}、c_2 = c_ {BA}$。 結合の値は既知であると想定されています-それらを通して、他のすべての量を表現します。

フルラプラシアン $$$Lm$オルソセンターの座標を含む $$$[rz、az、bz]$：

$$$Lm = \ begin {bmatrix} rz＆az＆bz \\ az＆c_1＆-c_1 \\ bz＆c_2＆-c_2 \ end {bmatrix}$

ここに $$$rz$-オルソセンターのノルム（対称の場合は半径の二乗として解釈されます）、 $$$az$そして $$$bz$-基準に基づくオルソセンターの分解の係数 $$$A、B$（重心の重み）。

完全グラミアン $$$Gm$次のようになります。

$$$Gm = \ begin {bmatrix} 0＆za＆zb \\ 1＆0＆g_1 \\ 1＆g_2＆0 \ end {bmatrix}$

タプルはこちら $$$[za、zb]$そして $$$[1、1]$nullベクトルの二重座標を反映します。 これらの座標は、ラプラシアンの消滅です （ラプラシアンを掛けると、ゼロベクトルを与えます-ゼロベクトルと混同しないでください！）。

問題を解決するには、グラミアンの値の合計を見つける必要があります。 $$$-（g_1 + g_2）$。

未知数の数を考慮します： $$$rz、az、bz、za、zb、g_1、g_2$-わずか7（はい、はい-不幸な距離の値を見つけるには、さらに7つの追加の値を計算する必要があります）。 入り口には2つの有名な接続があります- $$$c_1$そして $$$c_2$。 アイデンティティ $$$Lm \ Gm = I$9つの方程式が得られます。 合計7 + 2 = 9-すべてが収束します（驚くほど）。 方程式系を単純に解くことが残っています。

2つのノードのグラフの場合、解（すべての未知数）を明示的に表現できます。 関心のある量の有限表現を与えます。 一般的な幾何学的連結性の概念を紹介します -これは直交中心のノルムの逆数です $$$gc = 1 / rz$。 その次元は、グラフリンクの次元と一致します。 2つのノード（および2つの接続）のグラフの場合、幾何学的接続には次のような表現があります。

$$$gc = 1 / rz =（\ sqrt {c_1} + \ sqrt {c_2}）^ 2$

この接続により、ノードのスカラー積を表現できます。

$$$g_1 = -gc \ sqrt {c_2}、\ quad g_2 = -gc \ sqrt {c_1}$

スカラー積を翻訳できます $$$g$方向の距離で $$$s$（3）：

$$$s_ {BA} = gc \ sqrt {c_ {AB}}; \ quad s_ {BA} = gc \ sqrt {c_ {AB}}$

ノード間の望ましい可換距離は、合計によって決まります。

$$$S（A、B）= s_ {BA} + s_ {AB} = 1 / \ sqrt {c_ {AB} c_ {BA}} \ quad（4）$

おばあちゃんが到着しました

最後に。 式（4）-これは望ましい式です。

2つのノードのグラフの頂点間の距離は、カウンターリンクの積の平方根に反比例します。

別の役に立たない数式で学校の教科書を読み込むことができます。

接続が等しい場合、結果は無向グラフの抵抗距離と一致します。

$$$S_ {c、c}（A、B）= 1 / c \ quad（4.1）$

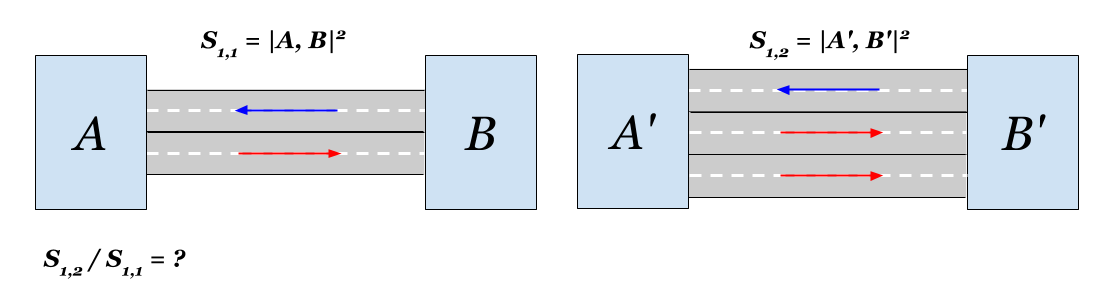
私たちは町に何があるかを計算します。 2番目のストリップを配置すると、1方向の接続が2倍になります。 したがって、新しい距離 $$$S_ {1、2}（A、B）$元の用語で表現できます：

$$$S_ {1、2}（A、B）= 1 / \ sqrt {2 c_ {AB} c_ {BA}} = 1 / \ sqrt {2} S_ {1、1}（A、B）$

エリア間の距離は減少します $$$\ sqrt {2}$回。 当たり前だったよね？

また、距離の観点から、各側の2車線道路に1車線を追加することは、片側に3車線を追加することと同じであることがわかります。 両方の場合のユークリッド近接性は2倍になります。 面白い。



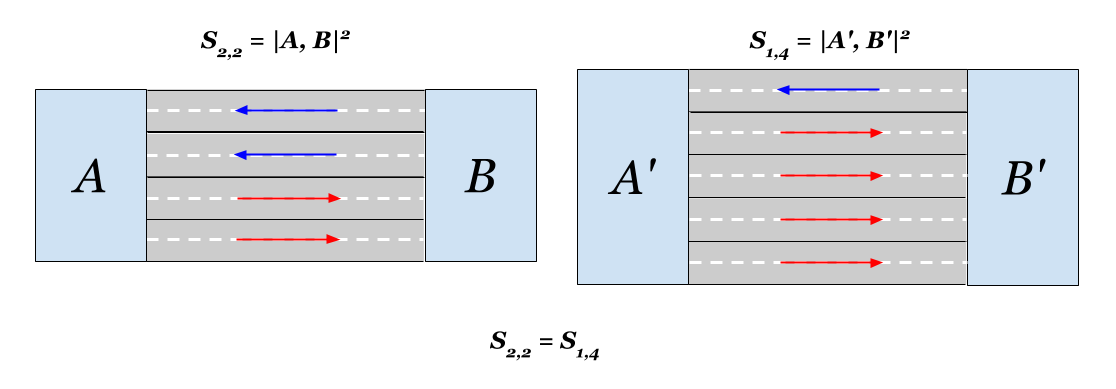
以上です。 ご清聴ありがとうございました。