まえがき
少し前まで、ポリゴンチェーン(
ポリラインポイントの数を減らすことができるプロセス)を単純化
する必要がありました 。 一般に、このタイプのタスクは、ベクターグラフィックスの処理時およびマップの構築時に非常に一般的です。 例として、いくつかのポイントが同じピクセルに分類されるチェーンを取ることができます。これらすべてのポイントを1つに単純化できることは明らかです。 少し前に、私は「完全に」という言葉からこのことについて事実上何も知らなかったため、このトピックに関する必要な知識をすぐに満たす必要がありました。 しかし、インターネット上でインターネット上に十分な完全なマニュアルを見つけられなかったとき、私は驚きました...私は完全に異なるソースからの抜粋を検索し、分析後、すべてを全体像に構築しなければなりませんでした。 正直言って、職業は最も楽しいものではありません。 したがって、多角形チェーン単純化アルゴリズムに関する一連の記事を書きたいと思います。 最も人気のあるDouglas-Peckerアルゴリズムから始めることにしました。
説明
アルゴリズムは、初期ポリラインと最大距離(ε)を設定します。これは、元のポリラインと単純化されたポリラインの間(つまり、元のポイントから結果のポリラインの最も近いセクションまでの最大距離)になります。 このアルゴリズムは、ポリラインを再帰的に分割します。 アルゴリズムの入力は、εの値だけでなく、最初と最後の間のすべてのポイントの座標(それらを含む)です。 最初と最後のポイントは変更されません。 その後、アルゴリズムは最初と最後で構成されるセグメントから最も遠いポイントを見つけます(
検索アルゴリズムはポイントからセグメントまでの距離です)。 ポイントがε未満の距離にある場合、まだ保存用にマークされていないすべてのポイントはセットから排出され、結果の直線は少なくともεの精度で曲線を滑らかにします。 この距離がεよりも大きい場合、アルゴリズムは開始点から指定された点まで、およびこれから終了点までのセットで再帰的に呼び出します。
Douglas-Peckerアルゴリズムは、作業中にトポロジを保持しないことに注意してください。 これは、結果として、自己交差する線を取得できることを意味します。 説明のための例として、次の点のセットを持つポリラインを使用します。[{1; 5}、{2; 3}、{5; 1}、{6; 4}、{9; 6}、{11; 4}、{13; 3}、{14; 2}、{18; 5}]そして、εの異なる値の単純化プロセスを見てください。
提示されたポイントのセットからの元のポリライン:

εが0.5のポリライン:
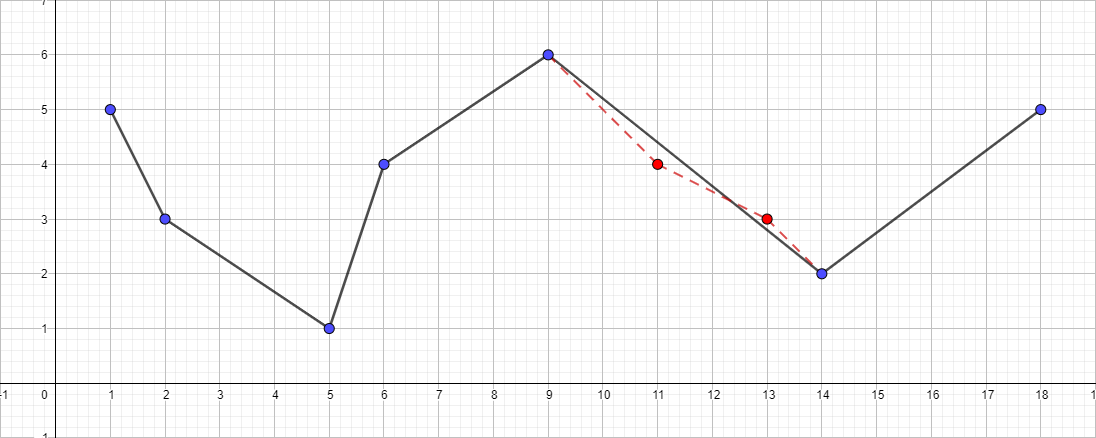
εが1に等しいポリライン

εが1.5に等しいポリライン:
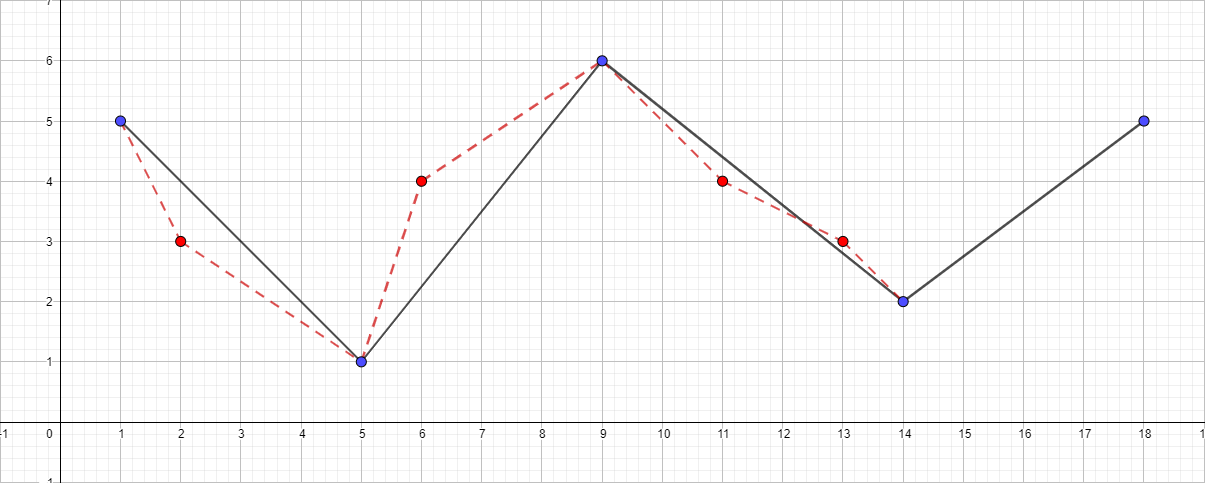
引き続き最大距離を増やしてアルゴリズムを視覚化できますが、これらの例の後の主なポイントが明らかになったと思います。
実装
C ++は、アルゴリズムの実装用のプログラミング言語として選択されました。アルゴリズムの完全なソースコードは、
こちらをご覧
ください 。 そして今、実装自体に直接:
#define X_COORDINATE 0 #define Y_COORDINATE 1 template<typename T> using point_t = std::pair<T, T>; template<typename T> using line_segment_t = std::pair<point_t<T>, point_t<T>>; template<typename T> using points_t = std::vector<point_t<T>>; template<typename CoordinateType> double get_distance_between_point_and_line_segment(const line_segment_t<CoordinateType>& line_segment, const point_t<CoordinateType>& point) noexcept { const CoordinateType x = std::get<X_COORDINATE>(point); const CoordinateType y = std::get<Y_COORDINATE>(point); const CoordinateType x1 = std::get<X_COORDINATE>(line_segment.first); const CoordinateType y1 = std::get<Y_COORDINATE>(line_segment.first); const CoordinateType x2 = std::get<X_COORDINATE>(line_segment.second); const CoordinateType y2 = std::get<Y_COORDINATE>(line_segment.second); const double double_area = abs((y2-y1)*x - (x2-x1)*y + x2*y1 - y2*x1); const double line_segment_length = sqrt(pow((x2-x1), 2) + pow((y2-y1), 2)); if (line_segment_length != 0.0) return double_area / line_segment_length; else return 0.0; } template<typename CoordinateType> void simplify_points(const points_t<CoordinateType>& src_points, points_t<CoordinateType>& dest_points, double tolerance, std::size_t begin, std::size_t end) { if (begin + 1 == end) return; double max_distance = -1.0; std::size_t max_index = 0; for (std::size_t i = begin + 1; i < end; i++) { const point_t<CoordinateType>& cur_point = src_points.at(i); const point_t<CoordinateType>& start_point = src_points.at(begin); const point_t<CoordinateType>& end_point = src_points.at(end); const double distance = get_distance_between_point_and_line_segment({ start_point, end_point }, cur_point); if (distance > max_distance) { max_distance = distance; max_index = i; } } if (max_distance > tolerance) { simplify_points(src_points, dest_points, tolerance, begin, max_index); dest_points.push_back(src_points.at(max_index)); simplify_points(src_points, dest_points, tolerance, max_index, end); } } template< typename CoordinateType, typename = std::enable_if<std::is_integral<CoordinateType>::value || std::is_floating_point<CoordinateType>::value>::type> points_t<CoordinateType> duglas_peucker(const points_t<CoordinateType>& src_points, double tolerance) noexcept { if (tolerance <= 0) return src_points; points_t<CoordinateType> dest_points{}; dest_points.push_back(src_points.front()); simplify_points(src_points, dest_points, tolerance, 0, src_points.size() - 1); dest_points.push_back(src_points.back()); return dest_points; }
さて、実際にはアルゴリズム自体の使用:
int main() { points_t<int> source_points{ { 1, 5 }, { 2, 3 }, { 5, 1 }, { 6, 4 }, { 9, 6 }, { 11, 4 }, { 13, 3 }, { 14, 2 }, { 18, 5 } }; points_t<int> simplify_points = duglas_peucker(source_points, 1); return EXIT_SUCCESS; }
アルゴリズム実行例
入力として、以前の既知のポイントセット[{1; 5}、{2; 3}、{5; 1}、{6; 4}、{9; 6}、{11; 4}、{13; 3}、{14; 2}、{18; 5}]およびεは1に等しい
- セグメント{1;から最も遠い点を見つけます。 5}-{18; 5}、このポイントはポイント{5; 1}。
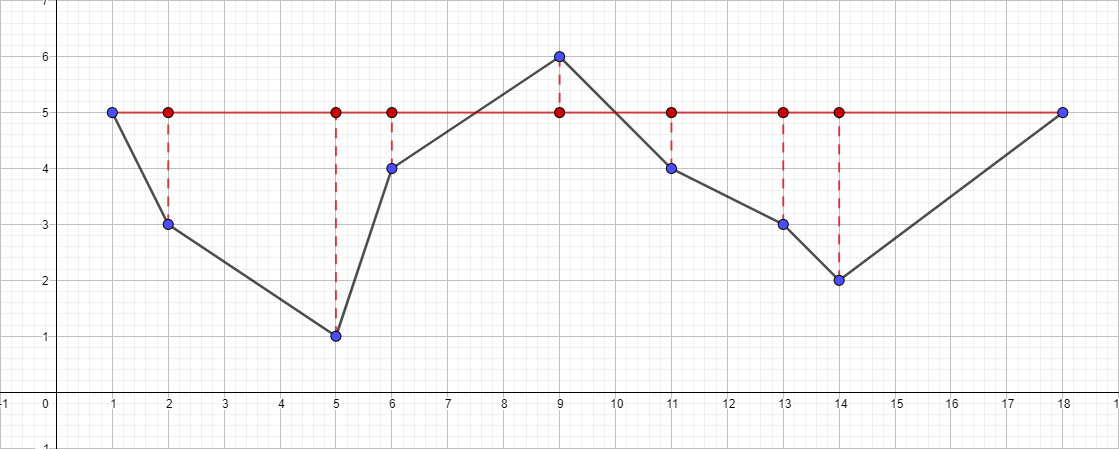
- セグメントまでの距離を確認してください{1; 5}-{18; 5}。 結果は1より大きいため、結果のポリラインに追加します。
- セグメント{1;のアルゴリズムを再帰的に実行します 5}-{5; 1}このセグメントの最も遠いポイントを見つけます。 この点は{2; 3}。
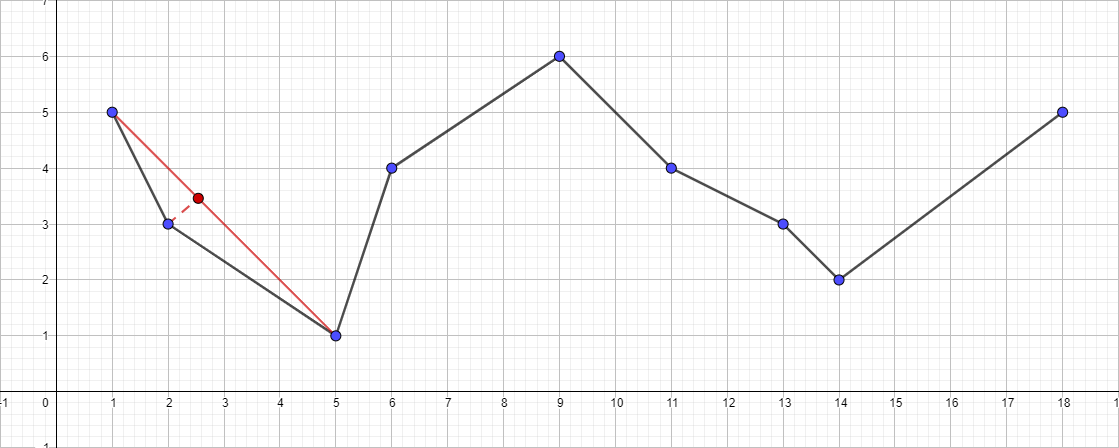
- セグメントまでの距離を確認してください{1; 5}-{5; 1}。 この場合、1未満であるため、このポイントを安全に破棄できます。
- セグメント{5;のアルゴリズムを再帰的に実行します。 1}-{18; 5}そして、このセグメントの最も遠いポイントを見つけます...
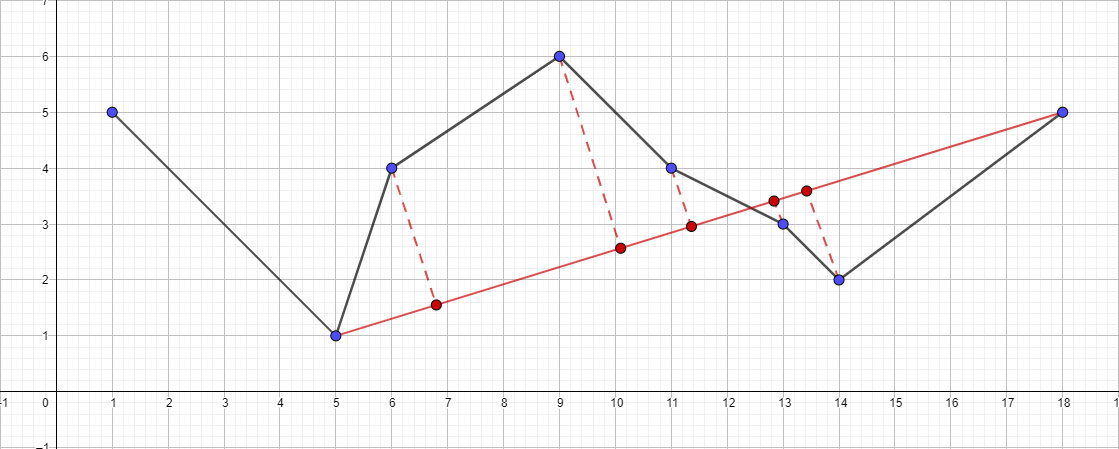
- 同じ計画に従って...
その結果、このテストデータの再帰呼び出しツリーは次のようになります。
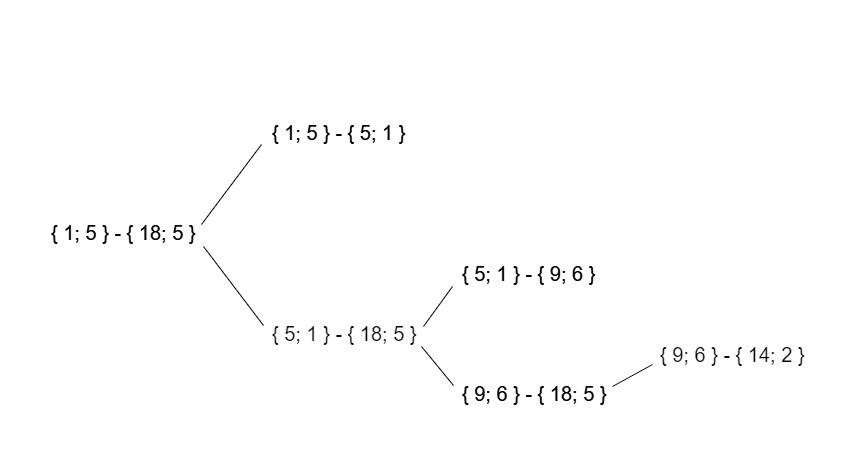
作業時間
アルゴリズムの予想される複雑さはせいぜいO(nlogn)です。これは、最も遠い点の数が常に辞書式に中心になる場合です。 ただし、最悪の場合、アルゴリズムの複雑さはO(n ^ 2)です。 これは、たとえば、最も遠いポイントの番号が常に境界ポイントの番号に隣接している場合に実現されます。
私の記事が誰かに役立つことを願っていますが、読者が十分な関心を示している場合は、すぐにReumman-Witkam、Opheim、Langの多角形チェーンを単純化するアルゴリズムを検討する準備ができているという事実にも注目したいと思います。 ご清聴ありがとうございました!