実験的に得られた定常時系列を分析する場合、原則として、データの予備準備（前処理）中に、それらに存在する傾向を抑制することが必要になります。
ここでは、非常に複雑なタイプの傾向に適したシンプルで明白な「新しい」傾向強調方法を提案します。
傾向は通常、プロセスの定常性を急激に侵害する超低周波の非調和成分として理解されます。 実験的に得られたデータの傾向の最も一般的な原因は、記録装置の「ゼロドリフト」です。 データの統合と他のいくつかのタイプの処理も傾向を引き起こす可能性があります。 トレンドの存在は、その後のデータ処理（スペクトル推定など）の結果を大きく歪めるため、トレンドの除去が必要です。 場合によっては、トレンド自体が貴重な情報源になります（たとえば、経済プロセスまたは気象プロセスの長期トレンドを分析する場合）。
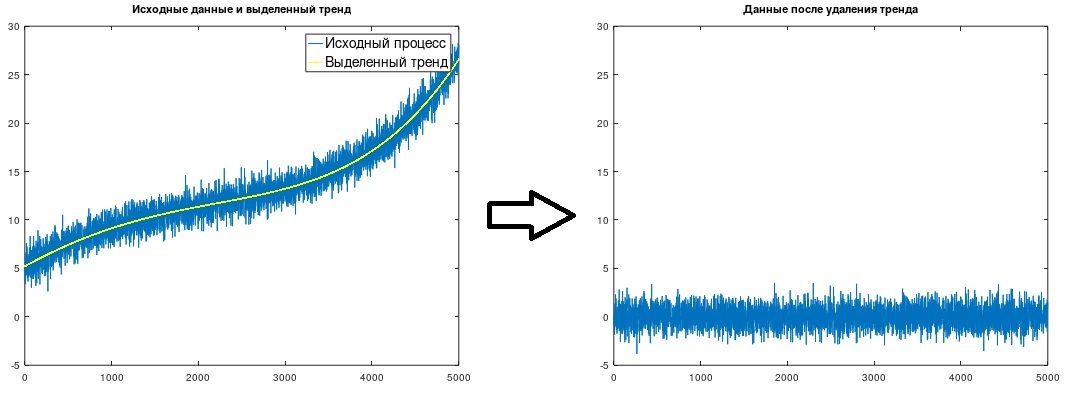図 1.トレンドの分離と削除通常、トレンドは線形関数または累乗（2次または3次）関数を使用してモデル化され、その係数はプロセスに特定のシーケンスを乗算し、最小二乗法を使用して導出されたかなり複雑な式を適用することによって計算されます。 （たとえば、J。Bendat、A。Pirsol、「Applyed Analysis of Random Data」、M.、Mir、1989を参照してください）。また、必要な依存関係を取得するためにディレクトリへの参照や独立した複雑なシンボリック計算を必要とせず、あらゆる種類の関数でトレンドをモデル化できます。 この変更された方法は非常にシンプルで明白なので（一度マスターしたら、スクリプトをメモリから書き込むことができます）、おそらく複数の異なる研究者によって「発明」されたことがありますが、これまでのところ出会ったことはありません。
トレンドを強調するために、N + 1個のサンプルで構成される初期プロセスx [i]の近似は、トレンド関数u
j [i]の少数のkコンポーネントを使用して実行されます。
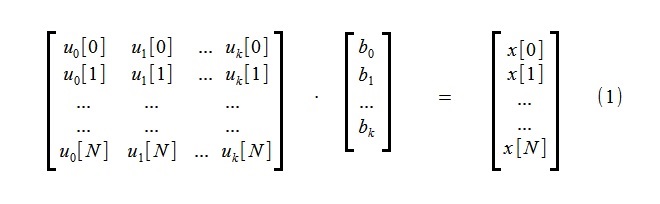
（通常、べき関数は関数u
j [i]として選択され、
しかし、この方法では絶対に原理的ではありません）
線形代数方程式系（1）には、k個の未知のb
jおよびN + 1の方程式が含まれます。
表記を取る：
もっとコンパクトに書く
過決定システムの近似解の検索における最小二乗法の適用は、次のように行列形式で記述されます。
スクリプトを記述するとき：当然、大きな行列U全体を保存する必要はありません。行列U
T UおよびベクトルU
T xの要素は、段階的に「累積」できます。
k個の方程式とk個の未知数のシステム（4）は、明白な方法で解決されます-たとえば、次のように記述します。
次に、見つかったb
jを使用して、次の形式でトレンドθ[i]を構築できます。
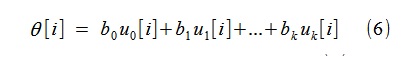
たとえば、フォームのランダムプロセスx [i]がシミュレートされました。
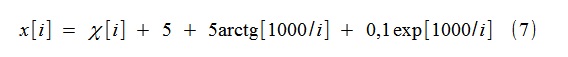
ここで、χ[i]-単一分散のガウス白色ノイズ。 傾向は、4次（k = 4）までのタイプ（2）（より正確には（8））の関数によってモデル化されます。
傾向のモデリングにべき法則関数を使用する場合、行列U
T U（4）はこれらの関数の線形独立性により理論的に常に可逆であることに注意する必要がありますが、高次のk（または非常に長いNのそれほど重要ではない）絶対価値が大きい。 kの高次では、計算が困難な場合、（8）などの低下係数を使用することをお勧めします。
（Δt= 1）、考慮された例で行われました。 図1に示す傾向が得られます。
トレンドを強調した後、当然、ソースデータから単純に差し引く必要があります。
発言。 通常、信頼できる情報源は、k = 2（正方形放物線）を超える次数のトレンドモデルを使用することを推奨しません。 これが従来の方法で「振幅」係数b
jを決定するのが難しいためか、上記のマシン変数の次数が使い果たされるか、プロセスの有益なコンポーネントをトレンドに誤って割り当てるかは、あまり明確ではありません。 与えられた例では、4次の傾向がかなり妥当であるかのように強調表示されています（ただし、3次の傾向と大差はありません）。 特に困難な場合には、ソースは別の方法を使用することをお勧めします-ローパスフィルタリング（ここでは考慮しません）。
上記のように傾向を強調すると、手順はそれほど複雑ではなく、「遅い」傾向を選択して分析するか、より頻繁に、高品質のデータ「出力」を取得するのに役立ちます-さらなる分析に適した中心定常定常プロセス。