多彩で完璧なハッシング

今週は、 「開発者向けアルゴリズム」コースの開始に役立つ有用な資料から始まります。 読書をお楽しみください。



1.概要

ハッシュは、興味深い微妙な理論を持つ優れた実用的なツールです。 語彙構造としてデータを使用することに加えて、暗号化や複雑性理論など、さまざまな分野でハッシュが発生します。 この講義では、2つの重要な概念について説明します。ユニバーサルハッシュ（ハッシュ関数のユニバーサルファミリーとも呼ばれます）と理想的なハッシュです。

この講義で強調されている資料には以下が含まれます。

• 正式な設定とハッシュの一般的な考え方。
• ユニバーサルハッシュ。
• 完全なハッシング。

2.はじめに

前に説明した辞書の主な問題を検討し、静的と動的の2つのバージョンを検討します。

• Static ：多数のS要素が与えられた場合、検索をすばやく実行できるように保存します。
• たとえば、固定辞書。
• 動的 ：ここには、挿入、検索、および削除のリクエストのシーケンスがあります。 これらすべてを効果的に行いたいと思います。

最初の問題については、ソートされた配列とバイナリ検索を使用できます。 2番目の方法では、バランスの取れた検索ツリーを使用できます。 ただし、ハッシュは代替アプローチを提供します。これは多くの場合、これらの問題を解決するための最速かつ最も便利な方法です。 たとえば、AI検索用のプログラムを作成していて、再計算したときに同じ計算を繰り返さないように、すでに解決した状況（ボード上の位置または状態空間の要素）を保存するとします。 ハッシュを使用すると、この情報を簡単に保存できます。 暗号、ネットワーク、複雑性理論にも多くのアプリケーションがあります。

3.ハッシュの基本

ハッシュの正式な設定は次のとおりです。

• キーはいくつかの大きなUのセットに属します（たとえば、Uは最大長80アスキー文字のすべての文字列のコレクションであると想像してください）。
• Uには本当に必要なSキーがいくつかあります（キーは静的または動的のいずれでもかまいません）。 N = | S |としましょう。 NがUのサイズよりもはるかに小さいことを想像してください。たとえば、Sは、128 ^ 80よりもはるかに小さいクラスの学生名のセットです。
• サイズMの配列Aとハッシュ関数 hを使用して、挿入と検索を実行します：U→{0、...、M-1}。 要素xが与えられた場合、ハッシュの考え方は、A [h（x）]に格納することです。 Uが小さい場合（たとえば、2文字の文字列）、ブロックソートのようにxをA [x]に保存できることに注意してください。 問題は、Uが大きいため、ハッシュ関数が必要なことです。
• 衝突を解決する方法が必要です。 衝突は、2つの異なるキーxおよびyに対してh（x）= h（y）の場合です。 この講義では、Aの各要素をリンクリストとして定義することにより、衝突を処理します。 他にも多くの方法がありますが、ここで焦点を当てる問題には、これが最適です。 この方法は、連鎖方法と呼ばれます。 アイテムを挿入するには、リストの一番上に配置します。 hが適切なハッシュ関数である場合、リストが小さくなることを願っています。

ハッシュの優れた点の1つは、すべての辞書操作が非常に簡単に実装できることです。 キーxを検索するには、インデックスi = h（x）を計算し、A [i]のリストを見つけるまで（またはリストを終了して）調べます。 挿入するには、リストの一番上に新しいアイテムを配置するだけです。 削除するには、リンクリストで削除操作を実行するだけです。 ここで、良いパフォーマンスを達成するために何が必要かという質問に移ります。

望ましいプロパティ。 適切なハッシュスキームに必要な主要なプロパティ：

1. キーは十分に分散されているため、衝突は検索時間と削除時間に影響するため、衝突が多すぎません。
2. M = O（N）：特に、テーブルMのサイズを要素数Nよりはるかに大きくすることなく、回路にプロパティ（1）を実現させたいと考えています。
3. 関数hは迅速に計算する必要があります。 今日の分析では、h（x）を定数として計算する時間を考慮します。 ただし、全体の実行時間に影響するため、複雑すぎないことを覚えておく価値があります。

この場合、要素xの検索時間はOです（リストのサイズはA [h（x）]です）。 削除についても同様です。 挿入には、リストの長さに関係なくO（1）時間かかります。 したがって、これらのリストの大きさを分析したいと思います。

基本的な直感：要素を美しく分配する1つの方法は、要素をランダムに分配することです。 残念なことに、次の要素をどこに向けるかを決定するために乱数ジェネレータを使用することはできません。それは、それを再び見つけることができないからです。 したがって、hを形式的な意味で「擬似乱数」にしたいのです。

ここで、悪いニュースをいくつか示し、次に良いニュースを示します。

ステートメント1（悪いニュース）任意のハッシュ関数h if | U | ≥（N -1）M +1、すべてが1か所でハッシュされたN個の要素のセットSがあります。

証明：ディリクレ原理による。 特に、カウンターポイントを考慮するために、各ロケーションがハッシュするUのN-1個以下の要素を持っている場合、UはM（N-1）以下のサイズを持つことができます。

これが、部分的にハッシュがとても神秘的なように見える理由です-ハッシュ関数について、それを防ぐ方法を考えることができるなら、どのようにハッシュが良いと主張できますか？ 1つの答えは、典型的なSセットに対して実際にうまく機能する多くの単純なハッシュ関数があるということです。

重要なアイデアは次のとおりです。ランダム化されたクイックソートと同様に、hコンストラクトでランダム化を使用しましょう。 （言うまでもなく、hは決定的な関数になります）。 挿入操作と検索操作のシーケンスについて（挿入された要素のセットSがランダムであると仮定する必要はありません）、この確率論的な方法でhを選択すると、このシーケンスでのhのパフォーマンスが期待できることを示します。 したがって、これはランダム化されたクイックソートまたはトラップと同じ保証です。 特に、これはユニバーサルハッシュの考え方です。

このアイデアを開発したら、「パーフェクトハッシュ」と呼ばれる特に楽しいアプリケーションに使用します。

4.ユニバーサルハッシュ

定義1.ハッシュ関数hを構築するためのランダム化アルゴリズムH：U→{1、...、M}
Uのすべてのx！= yについて



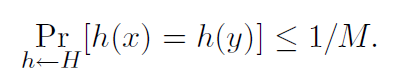
また、「h∈Hをランダムに選択する」手順が普遍的である場合、ハッシュ関数のセットHはハッシュ関数の普遍的なファミリーであると言えます。 （ここで、セット全体に均一な分布を持つ関数のセットを特定します。）

定理2. Hが普遍的である場合、サイズNの任意のセットS for U、任意のx∈U（たとえば、探すことができる）、Hに従ってランダムにhを構築する場合、xと他の衝突の予想数Sの要素はN / M以下

証明：各y∈S（y！= X）には、「ユニバーサル」の定義により、最大で1 / Mのxとの衝突の可能性があります。 だから

• xとyが衝突する場合はCxy = 1、そうでない場合は0とします。
• Cxがxの衝突の総数を示すようにします。 したがって、Cx =Py∈S、y！= X Cxy。
• E [Cxy] = Pr（xとyが衝突する）≤1 / M
• したがって、期待の線形性では、E [Cx] = Py E [Cxy] <N / Mです。

次の結果が得られます。

帰結3. Hが普遍的である場合、一度にシステム内にM個以下の要素しか存在できない挿入、検索、および削除操作Lのシーケンスでは、ランダムh∈Hに対するL操作の予想総コストはO（L）のみです（時間を表示hを定数として計算します）。

証明：シーケンス内の任意の操作について、その予想コストは定理2によって一定であるため、L操作の予想総コストは予想の線形性でO（L）です。

質問：ユニバーサルHを実際に構築できますか？ そうでない場合、これはすべてかなり無意味です。 幸いなことに、答えはイエスです。

4.1。 ユニバーサルハッシュファミリの作成：行列法

キーがuビット長であるとします。 たとえば、テーブルMのサイズは次数2に等しいため、インデックスはM = 2bでbビット長です。

ここでは、hをランダムな行列0/1 b行u列として選択し、h（x）= hxを定義します。ここでmod 2を追加します。これらの行列は短く太いです。 例：



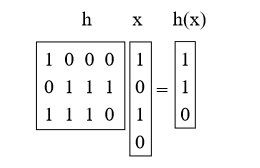
命題4. For x！= Y Prh [h（x）= h（y）] = 1 / M = 1/2 b。

証明：最初に、hをxで乗算するとどうなりますか？ これは、hの列の一部を追加する（ベクトル加算mod 2を行う）と考えることができます。xの1ビットは、追加する列を示します。 （たとえば、上記のhの1列目と3列目を追加しました）

ここで、x！= Yとなる任意のキーペアx、yを取得します。 それらはどこかで異なるはずなので、たとえば、i番目の座標が異なります。具体的には、xi = 0およびyi = 1とします。i番目の列を除くすべてのhを最初に選択したとします。 i番目の列の残りのサンプルでは、​​h（x）が固定されています。 ただし、ib列の2bの異なる設定のそれぞれは、h（y）の異なる値を与えます（特に、この列のビットを1回回すたびに、対応するビットをh（y）に変えます）。 したがって、h（x）= h（y）の1 / 2bのチャンスが正確にあります。

同じく素数の乗算に基づいて、ユニバーサルハッシュファミリを構築する他の方法があります（セクション6.1を参照）。

次に考慮すべき問題は、集合Sを修正した場合、すべての検索に一定の時間がかかるようなハッシュ関数hを見つけることができるかどうかです。 答えはイエスであり、これは完全なハッシュのトピックにつながります。

5.完全なハッシュ

すべての検索がO（1）で行われる場合、ハッシュ関数はSにとって理想的であると言います。 指定されたセットSに対して完全なハッシュ関数を作成する2つの方法を次に示します。

5.1方法1：空間O（N2）での解

辞書SのサイズNが2次のサイズのテーブルが必要だとしましょう。次に、理想的なハッシュ関数を作成する簡単な方法を示します。 Hをユニバーサル、M = N2とする。 次に、Hからランダムなhを選択して、試してください！ 声明では、少なくとも50％の確率で衝突しないとしています。

命題5。Hが普遍的でM = N2の場合、Prh〜H（Sでの衝突なし）≥1/2。

証明：

•Sにはいくつのペア（x​​、y）がありますか？ 答えは：
•各ペアの衝突の確率は、普遍性の定義により≤1 / Mです。
•したがって、Pr（衝突あり）≤ / M <1/2。

これは、「誕生日のパラドックス」の反対側のようなものです。 日数が二乗した人の数よりもはるかに多い場合、同じ誕生日を持つカップルはいない可能性があります。

したがって、Hからランダムなhを選択し、競合が発生した場合は、新しいhを選択します。 平均して、これを行う必要があるのは2回だけです。 さて、O（N）スペースのみを使用したい場合はどうでしょうか？

5.2方法2：空間O（N）の解

O（N）空間で完全なハッシュを実現することができるかどうかの問題は、しばらくの間、「テーブルをソートする必要がありますか？」 つまり、固定セットの場合、線形空間でのみ一定の検索時間を取得できますか？ 2レベルのスキームでユニバーサルハッシュ関数の良いアイデアを使用して最終的に解決されるまで、一連のますます複雑な試みがありました。

方法は次のとおりです。 まず、ユニバーサルハッシュを使用してサイズNのテーブルにハッシュします。 これにより、いくつかの衝突が発生します（幸運でない限り）。 ただし、方法1を使用して各バスケットを再ハッシュし、バスケットサイズを2乗して衝突をゼロにします。 したがって、スキームは、最初のレベルhのハッシュ関数と最初のレベルのテーブルAがあり、次に2番目のレベルh1のN個のハッシュ関数h1 ...、hNと2番目のレベルA1のテーブルのN、...、....要素xを見つけるには、まずi = h（x）を計算し、次にAi [hi（x）]の要素を見つけます。 （実際にこれを行った場合、インデックスiと実際に競合がある場合にのみ2番目のステップを実行するようにフラグを設定できます。そうでない場合は、x自体をA [i]に入れますが、ここで心配しないでください。）

ハッシュ関数hがn個の要素Sを位置iにハッシュするとします。 （方法1を分析することにより）h1、...、hNを見つけることができることをすでに証明しているので、二次テーブルで使用される合計スペースはPi（ni）2です。次のような第1レベル関数hを見つけることができることを示します。 Pi（ni）2 = O（N）。 実際、以下を示します。

定理6.普遍集合Hから開始点hを選択すると、

Pr[X i (ni)2 > 4N] < 1/2. 

証明。 E [Pi（ni）2] <2Nであることを示すことでこれを証明します。 これは、マルコフの不等式から望むものを意味します。 （量が4Nを超える可能性がある1/2の確率さえあれば、この事実だけで期待値が2Nを超えているはずです。したがって、期待値が2N未満であれば、失敗の確率は低くなります1/2。）

さて、トリッキーなトリックは、この量を計算する1つの方法は、自分自身との衝突を含む、衝突のある順序付けられたペアの数を数えることです。 たとえば、バスケットに{d、e、f}がある場合、dは{d、e、f}のそれぞれと競合し、eは{d、e、f}のそれぞれと競合し、fはと競合します{d、e、f}のそれぞれ、したがって9が得られます。

 E[X i (ni)2] = E[X x X y Cxy] (Cxy = 1 if x and y collide, else Cxy = 0) = N +X x X y6=x E[Cxy] ≤ N + N(N − 1)/M (where the 1/M comes from the definition of universal) < 2N. (since M = N) 

したがって、Pi n2 i <4Nのようなものが見つかるまでHからランダムhを試し、この関数hを修正して、方法1のようにN個の二次ハッシュ関数h1、...、hNを見つけます。

6.さらなる議論

6.1別の汎用ハッシュ法

ユニバーサルハッシュ関数を構築する別の方法を次に示します。これは、前述のマトリックス法よりもわずかに効率的です。

マトリックス法では、キーをビットのベクトルと見なしました。 この方法では、代わりに、キーxを整数のベクトル[x1、x2、...、xk]と見なします。各xiが{0、1、...、M-1}の範囲にあるという唯一の要件があります。 たとえば、長さkの文字列をハッシュする場合、xiはi番目の文字（テーブルのサイズが少なくとも256の場合）またはi番目の文字のペア（テーブルのサイズが少なくとも65536の場合）になります。 さらに、テーブルMのサイズが素数である必要があります。 ハッシュ関数hを選択するには、{0、1、...、M-1}からk個の乱数r1、r2、...、pkを選択し、以下を決定します。

 h(x) = r1x1 + r2x2 + . . . + rkxk mod M. 

この方法が普遍的であるという証明は、行列法の証明とまったく同じ方法で構築されます。 xとyを2つの異なるキーとします。 Prh（h（x）= h（y））≤1 / M. x！= Yなので、xi！= Yiのようなインデックスiが存在する場合があります。 ここで、j！= Iのすべての乱数rjを最初に選択したとします。 h ′（x）= Pj6 = i rjxjとする。 したがって、riを選択すると、h（x）= h ′（x）+ rixiが得られます。 これは、xとyの間に正確に競合があることを意味します

 h′(x) + rixi = h′(y) + riyi mod M, or equivalently when ri(xi − yi) = h′(y) − h′(x) mod M. 

Mは素数であるため、mod Mの非ゼロ値で除算することは有効です（1からM -1までのすべての整数はMを法とする乗法の逆数を持ちます）。つまり、上記の式が成り立つM true、つまりri =（h ′（y）-h′（x））/（xi-yi）modM。したがって、このインシデントの確率は正確に1 / Mです。

6.2ハッシュの他の用途

要素の長いシーケンスがあり、リスト内にいくつの異なる要素があるかを確認するとします。 これを行う良い方法はありますか？

1つの方法は、ハッシュテーブルを作成し、各要素を検索して、テーブルにまだない場合は挿入することにより、シーケンスを1回通過させることです。 個々の要素の数は、単に挿入の数です。

リストが本当に巨大で、保存する場所がないのに、おおよその答えが適切な場合はどうでしょうか。 たとえば、私たちがルーターであり、通過するパケットの数を観察し、（およそ）いくつの異なる送信元IPアドレスが存在するかを確認したいとします。

これは良い考えです：ランダム関数のように振る舞うハッシュ関数hがあり、h（x）が0から1までの実数であると想像してみましょう。できることの1つは、最小値を追跡することですハッシュ値はこれまでに生成されています（したがって、テーブルはまったくありません）。 たとえば、キーが3,10,3,3,12,10,12であり、h（3）= 0.4、h（10）= 0.2、h（12）= 0.7の場合、0が得られます。 2。

実際、[0、1]でN個の乱数を選択すると、予想される最小値は1 /（N + 1）になります。 さらに、かなり近い可能性があります（いくつかのハッシュ関数を実行し、低値の中央値を取ることで推定値を改善できます）。

質問：毎回乱数を選ぶだけでなく、なぜハッシュ関数を使用するのですか？ これは、要素の総数だけでなく、さまざまな要素の数を考慮しているためです（この問題ははるかに簡単です。単にカウンターを使用するだけです）。

友達、この記事は役に立ちましたか？ コメントを書いて、4月25日に開催される一般公開日に参加してください。