こんにちは親愛なる読者！ クリス・ヘッカーの記事「物理学、次のフロンティア」の英語からの翻訳を紹介します。

初心者のJava開発者である私は、物理的なゲーム内エンジンを作成するための資料が英語のみで提供されているという事実に直面したため、この記事は翻訳されました。 シリーズにはさらに3つの記事があります。できるだけ早く投稿します。 素敵な読書を！

物理学の新しいフロンティア

毎年、ゲーム内のグラフィックスがよりリアルになっていることは間違いありません。 すでに今日、誰もがテクスチャマップを使用して3Dワールドを作成（または少なくともスクリーンショットを表示）し、1人のプロジェクトに取り組むのに十分な勤勉な人々が集まると、各開発者は1秒間に数十億のポリゴンのリアルなテクスチャとシャドウを描画できます。 技術的には、高レベルでゲームを作成するために何をすべきか残っていますか？ 「21日で3Dハードウェアの使い方を学ぶ」という本を持っているすべての開発者は、本当に印象的なゲームを作成できますか？

まったくありません。 高級開発者は、さまざまなテクノロジー（GUIの複雑さ、人工知能、ネットワーキングなど）の水準を引き上げ続けます。 もちろん、これはすべて非常に重要です。詳細を指定せずに真剣に議論することはできません。 それにも関わらず、すべてに適用可能なテクノロジーが1つあります。これは、私の意見では、近い将来に決定的な要因になるでしょう。

次の例を考えてみましょう。DukeNukem 3Dの初期レベルの1つで、これらの巨大な回転ギアを覚えていますか？



図1.ゲーム「Duke Nukem 3D」のスクリーンショット

それらの回転が周期的なアニメーションではなく、実際の物理的なエンジンによって記述されることを想像してください。 インディ・ジョーンズの映画のように、歯車の1つが特定の角度から外れ、背後の廊下を転がるのと同じように、歯車は突然ゲーム装飾以上のものになります。 または、ロケットランチャーからギアを撃った後、廊下を転がり落ちて、あなたを殺すために後ろに忍び寄ってきた友人を粉砕することを想像してください！ 物理エンジンはそのような状況を現実のものにします。

物理シミュレーションは、ゲームの世界全体を構成するものです。そのおかげで、「ここ」はここにあります。 世界のグラフィックスの魔法は、プレイヤーが他のプレイヤーやレベルの壁に侵入したり、質量と質量の瞬間が感じられない場合、ゲームプロセスに突入することを許可しません。 ディズニーのアニメーターは、この大衆の感情が良いアニメーションを悪いアニメーションから分離するものであることに気付きました。 フランクトーマスとオリージョンストンによると、ディズニーアニメーション：人生の幻想の叙事詩であるディズニーアニメーターは、スタジオにポスターをぶら下げているだけでも、常に次の質問を自問する必要があります。 ？」

しかし、今日ではほとんどすべてのゲームに物理エンジンがありますよね？ 間違いなく、これはあなたの車がゲームの世界の端から落ちないようにするものです。これは、キャラクターがジャンプしても宇宙に飛び込むことがなく、ロケットが近くで爆発したときにボートを横に投げます。 ただし、現代のゲームのほとんどの物理エンジンはかなり脆弱です。 彼らは車が世界の端から落ちないようにするタスクに対処するだけですが、彼らの能力はゲームを新しいレベルに引き上げるのに十分ではありません-難破した車の残骸がトラック上で爆発し、壁や他の車のロールを引き起こします。

しばしば無視されるその他の物理的効果には、接線攻撃の結果としての単純なねじれ効果から、静的にアニメーション化されたものとは異なり、ゲーム内のキャラクター自体がバランスを保ち、動くことです。 多くの開発者は、物理学を説明する数学を理解していないか、テクスチャマップの作成に忙しくて学習できないため、これらの可能性を無視していると考えています。 3Dを操作するためのハードウェアの猛攻撃が後者を処理し、新しいシリーズの記事を始めています。 最初の記事では、手続きについて説明します。 私たちのサイクルの終わりまでに、あなたは信じられないほどのリアリズム、または面白くて永続的なシュールレアリズムのおかげで、プレイヤーがゲームプレイに完全に没入したように感じる物理エンジンを作成できます。

警告！ 物理学=数学、興味深いプロジェクトを終わらせるには、両方を使用する必要があります。 これを恐れる前に、物理学を説明する数学はエレガントで美しいだけでなく、適用された性格も持っていることに注意してください。 つまり、数学の抽象数学ではありません。 使用する各方程式には、実際の物理的な意味があります。 物理モデルから方程式を作成し、代わりに方程式がモデルの時間内の振る舞いを教えてくれます。

大企業

物理学は幅広い科学分野です。 しかし、「ダイナミクス」と呼ばれる小さなセクション、またはより正確には「固体のダイナミクス」に本当に興味があります。 ダイナミクスは、関連するセクション-キネマティクス（時間の動きの原理）の観点から定義できます。 キネマティクスは、運動の原因や身体の位置に注目せず、単に運動を説明します。 反対に、ダイナミクスは、時間とともに変化する運動学の値に寄与する力と質量を表します。 飛行時間が10秒で、初速度が時速50キロメートルであり、軌道-直線-が運動学的問題である場合、野球ボールがどれだけ飛ぶか。 野球ボールがバットで打った場合、地球の重力場でどれだけ飛ぶか-これは動的な問題です。

ソリッドを記述するダイナミクスの部分は、シミュレートされたオブジェクトに追加する制約に関連しています。 シミュレーション中にソリッドボディの形状は変化しません。ボディはゼリーのようなものよりも木製または金属である可能性が高くなります。 たとえば、人物の各部分をソリッドボディから構築し、それらの間に靭帯を作成することにより、人の関節のある人物を作成できますが、緊張や同様の効果で骨が曲がることは考慮しません。 これにより、ボディの興味深い動的動作の品質を失うことなく、方程式を単純化できます。

ダイナミクスのこのような小さな部分を考慮しますが、剛体のダイナミクスには、本質を説明する一連の記事が必要です。 私たちは、力の作用下での平面剛体の動きを記述するためのコンピュータープログラミングの基礎を研究することから旅を始めます。 私は「コンピュータープログラミング」を繰り返し続けています。運動学と動力学のために書いた方程式に加えて、浮動小数点数を使った計算を使用してこれらの方程式を解く方法も学ぶからです。 次の記事以降でのみ2次元の世界を扱うため、「フラットソリッド」と言います。 原理-そして実際には単なる方程式以上-を3次元の世界に移すこともできますが、2次元の世界では間違いなくすべてがはるかに単純であるため、3次元の空間に入る自信ができるまでそこで学習します。 今後の記事では、回転の効果、身体の接触の処理、そしてもちろん、これらすべてを3次元の世界で行う方法について説明します。 まあ、十分な言葉！ さあ始めましょう！

デリバティブを使用する

これは驚くかもしれませんが、オブジェクトを単純に押して移動することはできません。 そんなナンセンスを書くためにこの雑誌をゴミ箱に捨てて、私とは反対のことを証明するのは間違っていると思いますが、本当です！ マガジンに圧力をかけるだけでは、空間内のマガジンの位置に直接影響を与えることはありません。 実際、圧力は速度にも直接影響しません。 実際に圧力が影響するのは、ジャーナルの加速であり、実際、それは科学の歴史の中で最も重要な結論の一つです。

興味深いことをするためにこの事実を使用するためには、まず体の位置と速度および加速度との関係について話す必要があります。 実際、これらすべての値は非常に密接に関連しています（おそらくご存知のとおり）。速度は時間の経過に伴う体の座標の変化の指標であり、加速度は速度の変化の指標です。 これらの量の経時的な変化を研究するための主要なツールは微分計算です。 これを理解したら、次に進みます。 あなたは数学が得意だと思います。 単純なスカラーおよびベクトル計算（微分および積分）のみを使用しますが、数学全体に精通している場合は不要ではありません。 参考までに、コンピューティングに関する私のお気に入りの本は、ThomasとFinneyによるCalculus with Analytic Geometryです。

座標、速度、加速度は、この記事で説明する運動学です。 2次元の世界でのソリッドの位置は、明らかに座標XとYのペアであり、身体の特定の点の空間の座標を示します。 座標ベクトルの導関数は速度ベクトルであり、ポイントが移動している方向（および、現在発生している回転を無視する場合はボディ）と、移動速度を示します。 ベクトル計算はベクトルの各要素のスカラー計算であるため、X座標の導関数はXに対する体の速度などです。 以下の表記を紹介します。 物体の座標をベクトルrとし、速度をベクトルvまたは素数のあるベクトルrとします。 方程式が得られます：

$$

$${{dx} \ over {dt}} = v = r '$$

式1

速度ベクトルを時間で区別すると、座標ベクトルが時間とともにどのように変化するかがわかります。 加速は類推によって決定されます。 これは、速度の一次導関数または座標ベクトルの二次導関数です。

$$

$${{d ^ 2 r} \ over {dt ^ 2}} = r '' = {{dr '} \ over {dt}} = {{dv} \ over {dt}} = v' = a$$

式2

加速度の積分により速度が得られ、加速度を2回積分することで座標が得られます。

運動学におけるこれらの関係は、オブジェクトの加速を見つけることができ、時間をかけてそれを統合して速度と座標を取得できることを示しています。 後で見るように、シミュレーションコードで何度も統合を行い、各フレームのソリッドの新しい位置を計算します。 やったー！

これは、分析的に統合できる1次元の世界の簡単な例です。 現在の位置を描画するために、最後のフレームの終わりから現在のフレームの時間までの座標変化を見つけたいということに同意しましょう。 次に、ソリッドの加速度は5任意単位/秒^ 2に等しいと言います。 最後のフレームの終わりからの経過時間を変数t（積分要素dt内）として使用します。

$$

$$v（t）=∫adt=∫5dt= 5t + C$$

式3

上記の式は、速度が最後のフレームから経過した時間の関数であることを示しています。 積分定数Cが見つかりました。これは、積分期間の開始時（t = 0）の初期速度に等しくなります。

$$

$$v（0）= 5（0）+ C$$

$$

$$v_0 = {C}$$

式4

$$

$$v（t）= 5t + v_0 {}$$

ここで、速度方程式を統合して座標を見つけます（再び、積分定数を忘れないでください）。

$$

$$r（t）=∫v（t）dt =∫5t+ v_0 dt = {{5} \ over {2}} t ^ 2 + v_0 t + r_0$$

式5

式5に基づいて、初期座標と速度（最後のフレームから取得）と経過時間がわかっている場合、指定された加速度だけで現在位置を見つけることができます。 入力変数は時間であり、関数の値は現在の位置です。 また、次のフレームの初期条件としてこれを使用できるように、最終速度を計算するために式4で時間を示します。

力があなたと共にありますように

これで、アニメーションを取得するために運動学方程式を統合するために加速度を正しく設定する必要があることに気付きました。 ステージ上のスピーカーの出力。 私が言ったように、何かを押すと、身体の加速のみに直接影響することを覚えていますか？ さて、「圧力をかける」は、「力を加える」というフレーズのe曲表現です-ダイナミクスの2つの重要な変数の1つ-そして今、ニュートンに力が加速に与える影響を調べることができます。 ニュートンの2番目の法則は、力Fと質量の導関数（ダイナミクスの2番目の大きさ）と速度の関係を結びます。 質量と速度の積は、「体の運動量」と呼ばれ、pで表されます。

$$

$$F = p '= {{dp} \ over {dt}} = {{d（mv）} \ over {dt}} = mv' = ma$$

式6

質量は現在作業中の速度の定数であり、これは式6の導関数から得られ、よく知られている式F = maを得ました（ただし、ニュートンは最初に運動量の導関数によって力を決定したと確信しています）。

マテリアルポイントのみを扱う場合、方程式6はダイナミクスに必要なものです。 与えられた質点の与えられた力に対して、加速度は力を質量で除算することで求められます。 これにより加速が得られ、上記の例の運動方程式を解くのに役立ちます。 それにもかかわらず、私たちは、特定の領域（3次元の世界ではボリューム）に分布する質量を持つ固体を扱っているため、まだ作業が必要です。

まず、固体を点の集合として考えます。 ソリッドの総運動量pTは、ボディを構成するすべてのポイントの運動量の合計として定義します（これらのポイントにどの定量値が属しているかをより明確に示すため、上位のインデックスを使用します）。

$$

$$p ^ T = \ sum_ {i} {m ^ i v ^ i}$$

式7

重心（CM）の概念を導入することにより、剛体のダイナミクスの解析を大幅に簡素化できます。 重心に向けられたベクトルは、固体のすべての質量点から導かれたベクトルの線形和を、全身の質量Mで割ったものです。

$$

$$r ^ {CM} = {\ sum_ {i} {m ^ i r ^ i} \ over {M}}$$

式8

重心の定義を使用して、式8の両側にMを乗算し、それらを微分し、結果を式7に代入することにより、式7を単純化できます。

$$

$${{d（Mr ^ {CM}）} \ over {dt}} = {\ sum_ {i} {} {{d（m ^ ir ^ i）\ over dt}}} = {\ sum_ {i} {} {m ^ iv ^ i}} = p ^ T$$

式9

式9の右側は、式7で定義されている総運動量です。次に、式の左側を見てみましょう。これは、質量中心の速度に全身の質量を掛けたものです。 右側を左側に移動して以下を取得します。

$$

$$p ^ T = {{d（Mr ^ {CM}）} \ over {dt}} = Mv ^ {CM}$$

式10

式10から、線形運動量は総質量に重心からの速度を掛けたものに等しいため、体の質量と重心の速度ベクトルの方向がわかっている場合、運動量を見つけるために式7で合計する必要はありません。 さらに、計算の最終結果はすべて全身の積分を見つけることですが、重心が存在し、式10からの総運動量の決定を大幅に簡素化します。したがって、心配することはできません-線形運動量を見つけるために、与えられた速度と質量をもつ物質点と見なすことができます。

類推により、総力は総運動量の導関数であるため、重心の概念を使用して力の方程式を単純化できます。

$$

$$F ^ T = p ^ T = Mv '^ {CM} = Ma ^ {CM}$$

式11

要するに、式11から、固体と相互作用するすべての力を、それらの合計ベクトルが全身の質量を含む重心の点に影響を与えるかのように考えることができることがわかります。 重心の加速度を見つけるために力（読み取り重力）をMで除算し、次に身体の速度と座標を取得するために加速度を時間で積分します。 なぜなら 次の記事まで回転の影響を無視します;剛体のダイナミクスを記述するために必要なすべての方程式が既にあります。 式11には、体に加えられた力の方向に関する情報が含まれていないことに注意してください。 これは、線形の運動量と重心を扱うときにポップアップし、CMに力を加えて重心の加速度を見つけるだけです。 次の記事でこれらの力の影響下で体の回転を計算すると、力の適用の座標がどのように使用されるかがわかります。

歓喜の歌

この段階では、方程式11を使用して、任意に選択した値= 5の代わりに重心の加速度を求める分析積分の別の例を検討できます。しかし、分析積分には通常、適用値がないため、深刻な問題に直面します複雑すぎるため、いわゆる常微分方程式（ODE）のいわゆる数値積分に焦点を当てます。 うわー、今では本当の数学のように聞こえます！ これを学んだら、バーを上げる時が来ます。 幸いなことに、ODEの数値積分は一見すると思えるほど難しくありません！ これが何を意味するのかを理解するために、私たちは言葉から行為に移ります！

したがって、微分方程式は、関数自体、独立変数、およびパラメーターに加えて、従属量の導関数を含む方程式です。 これは冗長ですが、1次元の世界で時変する力の例は次のとおりです。F= 2t、Fは従属量、tは独立です。 Fの値はFによってのみ決定されます。力の方程式は体の速度のみに依存します。 航空機の速度が増加すると、空気抵抗が増加します。 1次元の世界の例に戻りましょう。F= -vの場合、摩擦力が速度に比例して体を減速させるとしたらどうでしょうか。 次のように方程式を解くので問題があります：F = ma = -vそして、mで割ると、次のようになります（加速度は速度の導関数であることに注意してください）：

$$

$$a = {{dv} \ over {dt}} = {-v \ over m}$$

式12

この微分方程式（速度方程式には方程式12の速度微分が含まれます）は、従属量の常微分のみを含むため、常微分方程式と呼ばれます（偏微分方程式[UPC]を構成しますが、これについては説明しません） ）

次に、フレーズの次の部分である統合に移りましょう。この方程式の条件でvを見つけるために、以前dv / dtをどのように統合しましたか？

これは信じられないように思えますが、物理学のほぼすべての方程式は微分であるため、ODEはよく研究されています。多くの場合、定量的な量の変化率は量自体に依存するため、微分方程式は物理学でよく見られます。たとえば、空気抵抗の速度を含むブレーキ（速度の変化の大きさ）は速度に依存することを既に説明しました。物理学からの他の例：冷却（熱損失率は現在の温度に依存）および放射性崩壊（減衰率は放射性物質の量に依存します）。

私たちのフレーズの最後の言葉-数値-は私たちの救いです。これは、微分方程式の解析的積分の理論は、最も単純なものであっても、非常に大きく、混乱を招くためです。皮肉なことに、コンピューター数値法を使用してODEを統合することは、実際には比較的簡単に理解できます。次に、オイラー法に基づいた簡単な数値積分器について説明し、次の記事でそれを改良します。

ほとんどすべての数値積分器は、オイラー法ほど明確ではありませんが、傾斜の1次導関数による計算の古い定義に単純に基づいています。dy/ dxは、xに応じてyの勾配を決定します。たとえば、一次方程式y = 5xがある場合、dy / dx = 5は、任意のxに対して勾配が5に等しい定数であることを意味し、推測できるように、これは直線です。もう少し難しい例は、放物線y = x2です。この場合、dy / dx = 2xであり、これは各x座標の新しい傾きを決定する関数です。図2にy = x2を示しました。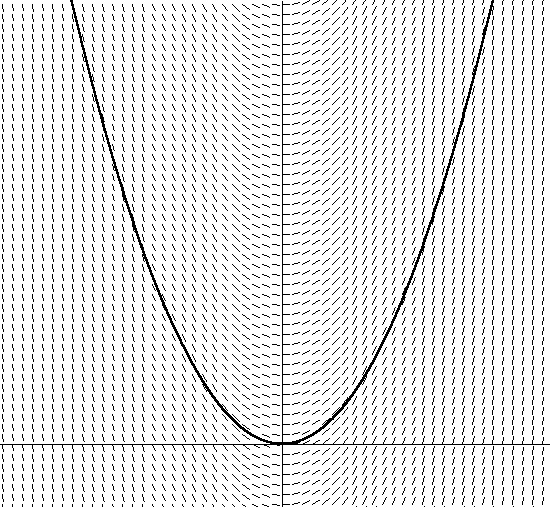



図2. y = x2

これに加えて、すべてのxについて方程式dy / dx = 2x + Cを解くことにより、斜めベクトルの方向もハッチングしました。傾斜ベクトルの角度は、この点での接線の角度の接線に等しいことに注意してください。また、接線のセットの角度を満たす多くの異なる放物線があり、y軸に沿ったシフトのみが異なることに注意してください。これらの放物線のそれぞれは、方程式dy / dx = 2x + Cに含まれる異なる積分定数を使用して取得されます。私が描写した放物線の積分定数は0です。たとえば、1のような別の定数を選択すると、方程式y = 2x +1。これは、y軸上に1単位シフトした同様の放物線があることを意味します。

ここで、放物線によって定義された図2のベクトルのフィールドがわからない場合は、水たまりに座ってください。そのため、接線方程式を解くには、各点でベクトルの方向に従う必要があり、ベクトル場の方向の変化に応じて方向を変えます。しばらくすると、どこから始めたかに応じて、放物線の軌跡に沿って（または放物線の一部に沿って）移動していることがわかります。気付かないうちに、ベクトル場の方程式を統合しました。微分方程式（ベクトル場内を移動する際のdy / dxの計算）のみを使用して、特定の放物線（開始位置または初期条件に依存）を見つけました。

実際の微分方程式に同じことをするのも簡単です。タイプdy / dx = f（x、y）の微分方程式の場合、微分dy / dxをf（x、y）の接線として求めると、グラフx、yの各座標の接線の傾斜角がわかります。 dy / dx = f（x、y）で与えられるベクトル場をプロットする場合、各点で導関数を見つけてその方向に進むことにより、放物線との類推でこれに従うことができます。図2は、空気抵抗の式である式12のベクトル場を示しています。速度は垂直軸に沿っており、時間は水平に沿っています（このグラフではm = 1を任意に選択しました）。



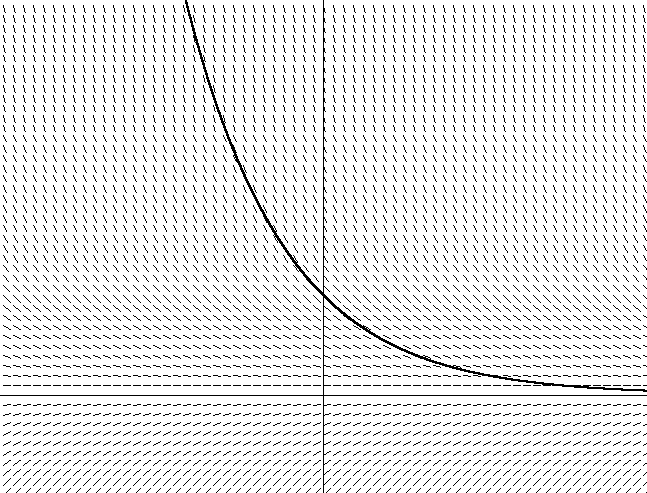図3. dv / dt = -v / m

また、多くの可能な曲線の1つを示しています。グラフの開始位置（方程式の初期速度に依存します）を選択すると、摩擦力がボディを減速させるため、時間がたつにつれて速度がゼロになる傾向があることに気付くかもしれません。また、速度の低下が速度の現在の値にどのように依存するかを確認することもできます。動きが速いほど、速度は低下します。これは、式12からも同じことがわかります。

数値積分は、チャートで行ったものと似ています。数値積分のオイラーアルゴリズムは、方程式の導関数（摩擦力を使用した例では-v / m）を見つけることにより、初期位置に従ってベクトル場をたどり、現在のポイントで勾配を決定します。勾配に沿ったhの変更されていない値。次に、特定の時間間隔の後、新しい勾配を決定するために新しい位置が計算されます。

$$

$$y_{n+1} ≈ y_{ n } + {h(dy_{ n })\over dx}$$

より正確には、空気抵抗の方程式：

$$

$$v_{ n+1 } ≈v_{ n }+{h( -v_{n})\over m}$$

明らかに、オイラー法は各時間ステップで小さな誤差を与えます。これは、実際の速度ベクトル（したがって解曲線）が各点で偏差を伴って曲がり、オイラーアルゴリズムが傾斜角からわずかに逸脱するためです。ただし、タイムステップhがかなり小さい場合、誤差はゼロになる傾向があります。これについては、今後さらに詳しく説明します。

オイラー法を使用した数値積分について知る必要があるのはこれだけです。速度をどのように統合して座標を取得するのかを尋ねることができます。同様に、オイラー法を再び使用して、dv / dt = aを統合したように、dr / dt = vを統合します。 2つの結合微分方程式が得られます（もう1つの勝利の方程式）。

$$

$$v_{n+1} ≈ v_n+hv'=v_n+{h F_n\over M }$$

$$

$$r_{ n+1 } = r_n + hr_n'= r_n+hv_n$$

これにより、オブジェクトに任意に加えられた力の作用後の座標を計算するための代替アルゴリズムが得られます（これは、見たとおりの速度、時間、または体と他の体の位置、またはすべてに一度に依存します！）。オイラー法では、いつでも計算できるため、適用される力がどのように見えるかは重要ではありません。オイラーは、質量に対する力の効果の大きさに興味がありますが、それだけです。
スペースが足りなくなったため、リンクを提供する方法がありません。次回はさまざまな素晴らしい本をアドバイスし、ソリッドの回転を計算する方法を見つけます。

そして、彼の体は私たちが望むほど堅実ではありませんが、クリス・ヘッカーはダイナミックな性格を持っています。あなたが力を加えると、彼は電子メールchecker@bix.comに答えます。

翻訳者のメモ：しゃれがここに表示され、記事のトピックとその内容が再生されます。

PS翻訳の著者は、翻訳を編集してくれたberezとMarazmDedのユーザーに特別な感謝を表明します。よろしくお願いします！