多数のセンサーによって貼り付けられた、フルスケールの動的テスト(たとえば、車両の振動活動を研究するとき)中の「研究オブジェクト」は、大量のデータを簡単に提供しますが、それをどう処理するかはあまり明確ではありません。 同じことは、多数の自由度を持つシステムの動的プロセスのシミュレーションモデリングでも発生します。
これは、定期的に問題に遭遇しない人には完全には明らかではないかもしれませんが、時間と空間で確率論的なプロセスの対応するアニメーションを見ることは、原則として、ほとんど意味がありません。 どこで壊れるのか、なぜそんなに揺れるのか-通常「見えない」。 彼らがアニメーション以外に思いついたものは、以下で説明しますが、これをお勧めします。
基本手順により、振動自体の空間的な「形」、さらに、与えられた荷重条件とその強度(分散、必要に応じてプロセス自体)の下で実際に現れるものも取得できます。
図1マルチチャネル応答の擬似フォームへの展開 「粘性媒体中のストリング」(図2を参照)
アニメーションに加えて、「ペアワイズ」スタディ(相互スペクトルなど)が知られていますが、もちろん一般的な状況はわかりません。
そのような方法は非常に明白です-スペクトログラムの共鳴ピークに対応するスペクトルの非常に狭い帯域を「カットアウト」することにより、スペクトログラム(再び「ペアワイズ」)方法は、ほぼ調和の(高度に相関した)振動のほぼ形を生成します。
明らかな技術的な複雑さに加えて、このような方法の欠点は、通常「参照」チャネルを「成功して」選択する必要があることです。これは常に可能とは限りません。 その結果、プロセスの相互フェーズで非常に大きなエラーが発生します。 さらに、線形システムの特性に起因する、振動の顕著な空間形式とそのようなエラーのないことは、「複雑」(非同相)であることが判明し、その後の主観的分析の値は通常(常にではない)大幅に減少します。
ねじれ振動の4チャネル研究(平均的なバスの搬送システム)が知られており、研究者のインスピレーションによって決定される振動の空間形式を使用して1つのプロセスで割り当てられます。それらは、軸対称に位置する他の2人の証言から差し引かれました(「-」から取得)。
センサーの数が少ない場合でも、このアプローチは完全に良いとは限りません。 たとえば、トラックのフレームは通常、エンジン下部(フロント)部分でより順応性が高く、ねじれ形状であり、おそらくより複雑な形式(おそらくフロントセンサーの「増加」係数を含む)を想定する必要があります-同時に、受け入れられたものを実証する問題モデル)。 監視チャネルの数が増えると、これはすべて非常に複雑になり、正当化が不十分になります。
別の実験またはシミュレーションから事前に決定されたいくつかの形式の振動(モード)の明示的な分離(プロセスへの)は、かつて(おそらく私だけではなく)私によって提案され、その後、私のチーフによって「モード分解の方法」と呼ばれました。 この方法でフィールドテストの結果を分析し、ベンチテスト(または有限要素モデリング)によって独自のフォームのベクトルを決定することが想定されていました。
実際に、彼らはこれについてしましたが、同時にそれが判明しました。
「立ち上がった実験者」は、「ポリゴン」の実験者とは対照的に、真の妨害プロセスの同期観測に利用できることは明らかです。 これにより、大きな利点が得られました-真の伝達関数を決定し、利用可能なハードウェアとソフトウェアを使用して、構造振動の独自の形式と周波数を実験的に決定できます(クーフィッティング、「目で」周波数範囲を「カット」し、システムにいくつの形式があるかを示します)見つける;科学よりもむしろ芸術だが、それでも)。
しかし。 彼らは明らかに、車の組み立て品などの物体の探索、別個のフレームの支持、車体の支持などを避けました。 -減衰が非常に低いオブジェクト。 モーダルベンチテスト-固有振動数と形状の決定についてです。 シミュレーションではありません。 わずかに強く減衰する物体の振動のもっともらしい固有モードは、実験的に実験的に取得できますが、かなり難しくなります。
非常に貴重な情報は、これらの「好み」に関するものであることが判明しました。 非常に簡単に言えば、その後徐々に結論に達した結論のみ:アイデアの「美しさ」にもかかわらず、応答を真の適切な構築形態に正確に分解しようとすることはほとんど価値がありません。
「指に」ある場合、その理由はおそらく高い確率です。たとえば、外乱に応じて、「自然振動モード」(より正確には、自然振動モードに対応する静止「モーダル」プロセス)は次のようになります。さもなければ、それらは相互に相関し、実際には他のいくつかの空間的形態の振動を、それら自身とはある程度異なるものに形成し、これは自然に構造の減衰への強い依存で現れます。
「反対から」簡単な説明として-2つの異なる「減衰されていない」高調波は、それ自体、常に何らかの形で無相関です。 (説明。前述の「独自の形式の混合」の効果は、「有意な非線形性」がない場合、および線形システムの「不均衡な」減衰を伴う「複雑な形式」の外部で観察されます。)
上記に基づいて、特定の形式の振動(曲げ、ねじれなど)など、いくつかの相関に依存しないプロセスの合計としてシステムの応答を提示することが提案されています。 このような分析は非常に単純であり、原則として、非常に貴重な結果が得られます。 得られた形式は、システムの振動の固有モードに似ている場合と似ていない場合がありますが、実際の外部影響の条件下でシステムの動作を常に正確に反映します。 さらに、それらは可能な限り単純で有益な情報を反映し、分散によってランク付けされたシーケンスは近似シリーズです。
関心のある分解を取得するために、(1)を考慮します。
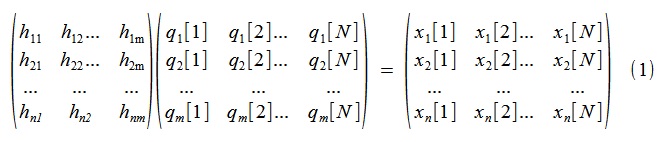
または、同じコンパクトに(2)、
ここで、
xは実験で直接得られたNサンプルの持続時間を持つシステムのnチャネル物理応答、
qは相互に相関のないチャネルを備えたmチャネル実「モーダル」プロセス、Hは希望の同相(「実」)振動モードを記述する列の行列です。
一般的に、m <nが後に期待されます(フォームの数は物理的応答チャネルの数より少ない)が、最初はm = nであると仮定し、Hと
qがランクnの場合、(2)はいずれの場合でも、残差なしで満たされ、明らかに
| H・Rqq [0]・H T = Rxx [0](3) |
またはより詳細に
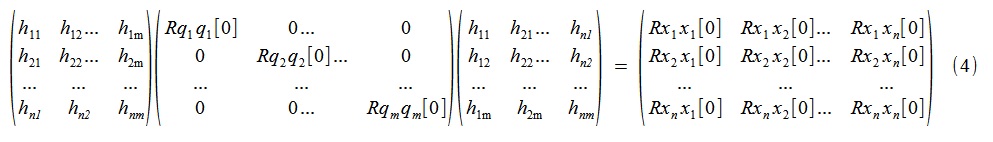
つまり、求められているそのような「擬似固有」振動モードおよび対応する無相関(ゼロラグ付き)プロセス
qの検索は、対称行列Rxx [0](プロセス
xの自己相関および相互相関の値で構成される)のスペクトル分解(固有ベクトルおよび数に関して) lagΔτ= 0)独自の正規直交ベクトルは望ましい形式を与え、実固有値は対応するプロセスの分散を与えます(重要なものに加えて、ほとんどの場合〜0の分散があるため、実際には通常m <n)。 必要に応じて、一時的な実現の形でプロセス自体を構築したり、それらのスペクトルを見つけたりすることができます。
上記を明確にするために、5自由度の線形機械システムのモデルを検討します。このモデルは、粘性媒体内の弦の挙動をほぼシミュレートします(図2)。
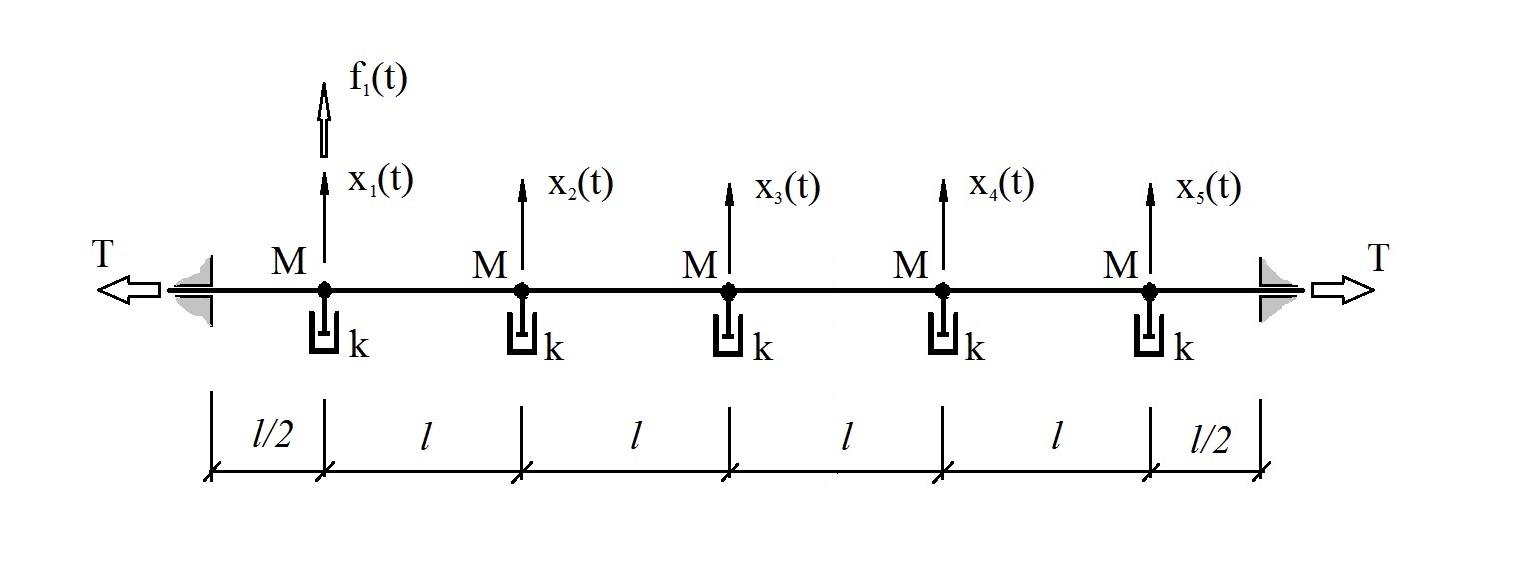 図2テストシステム
図2テストシステムピンクノイズのタイプの確率的外乱f
1 [i]の影響下で振動する(図3)、サンプリング間隔Δt= 0.01 s、実装長25000サンプル(以下、PSD推定値は、ウェルチ法、セグメント長1024、ハミングウィンドウが適用され、セグメントの60%のオーバーラップ。)
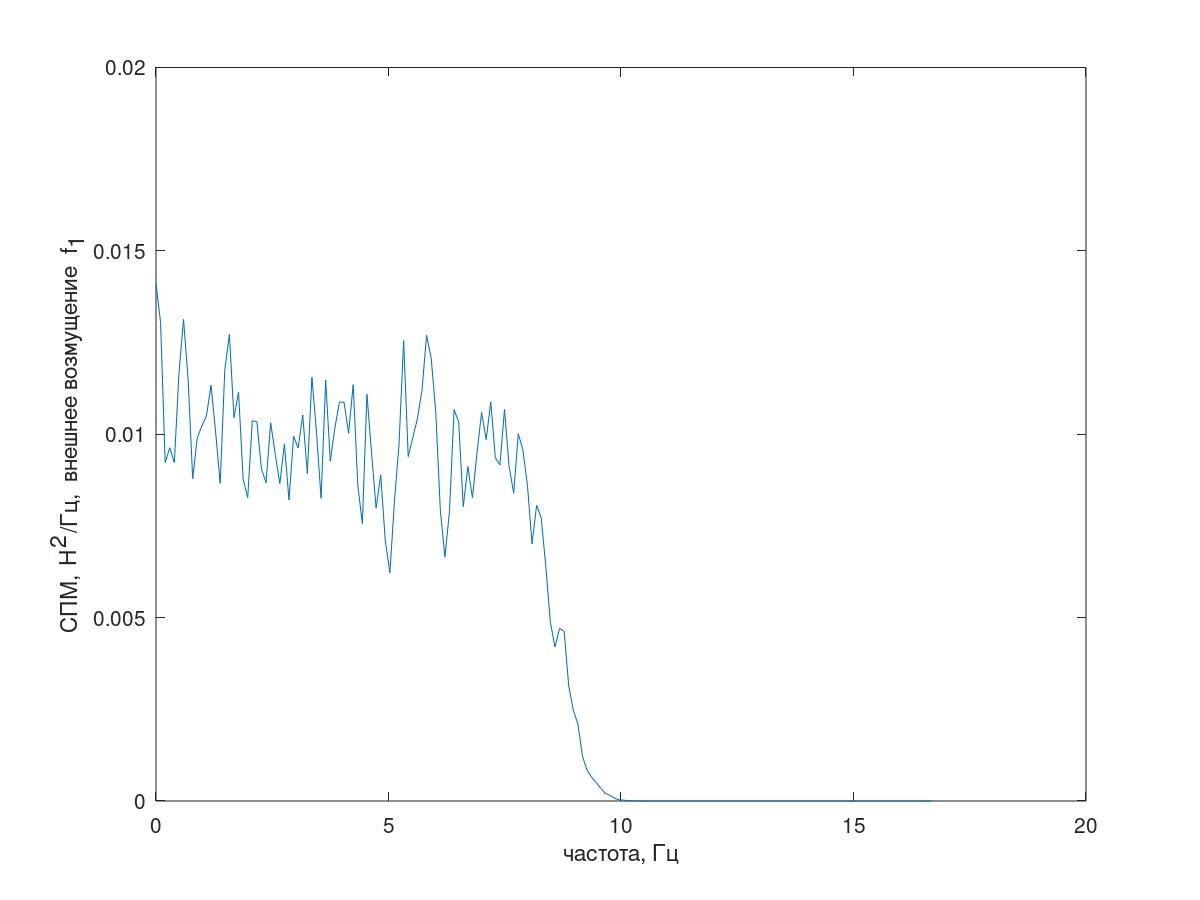 図 3外乱のスペクトル。
図 3外乱のスペクトル。
外乱の一時的な実装の一部を図4に示します。
図4入ってくる妨害の一時的な実装の断片
連続時間では、モデルは拡散方程式のシステムです(6)、
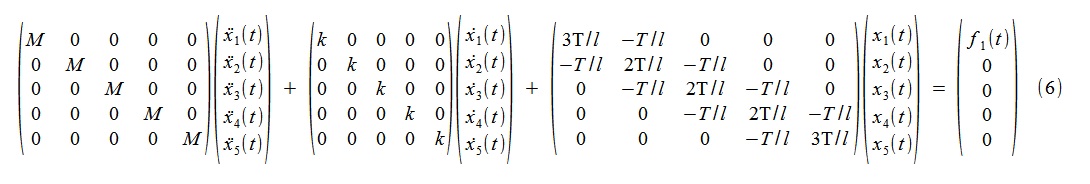
ここで、M = 1kg、k = 10kg / s、T = 2000N、l = 1mです。
対応する(明確な)行列は、数値的に次と等しい:

システムの周波数応答の1つを図5に示します。
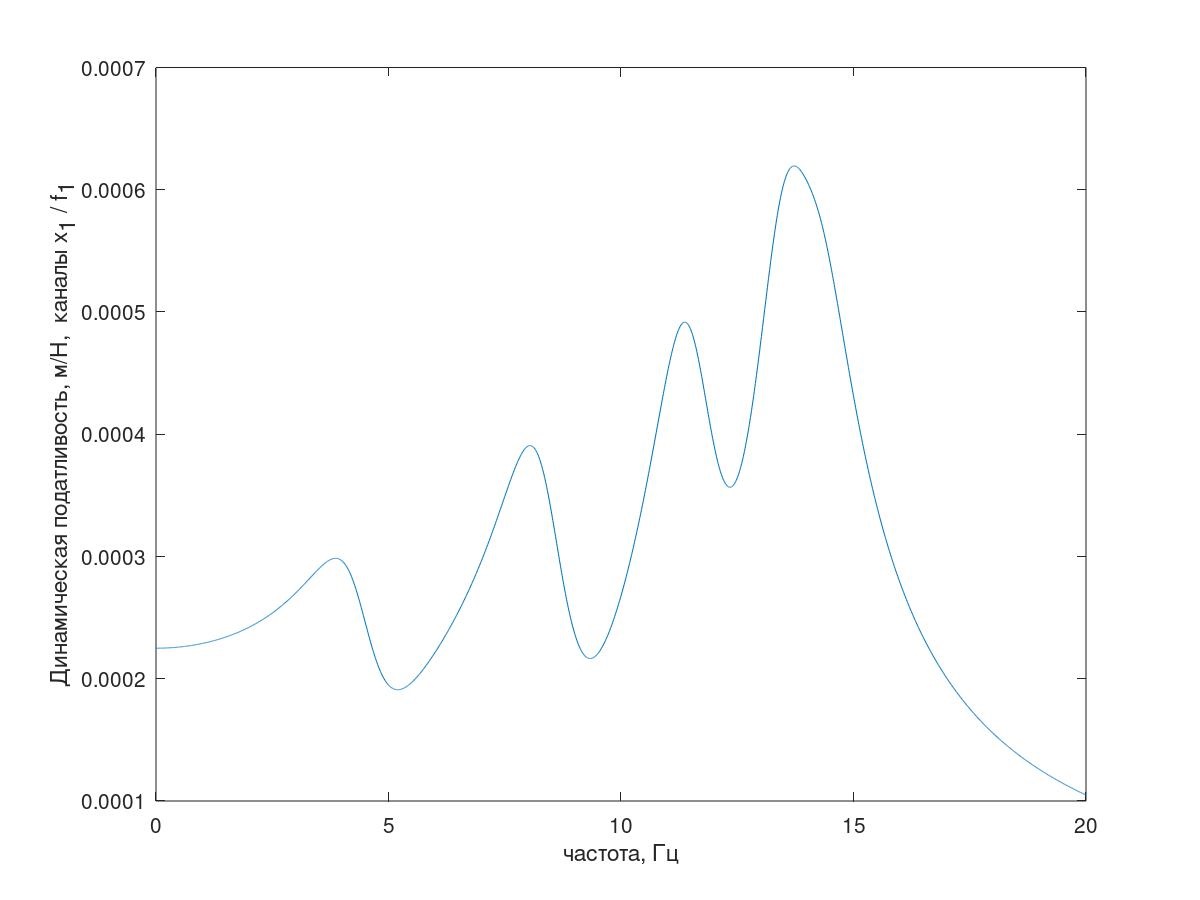 図5 テストシステムの周波数応答
図5 テストシステムの周波数応答(説明-条件付き減衰(k = 1 kg / s)を備えたシステムのこの周波数応答の説明が図5に示されているように、すべてが共振ピークの数の順序になっています)
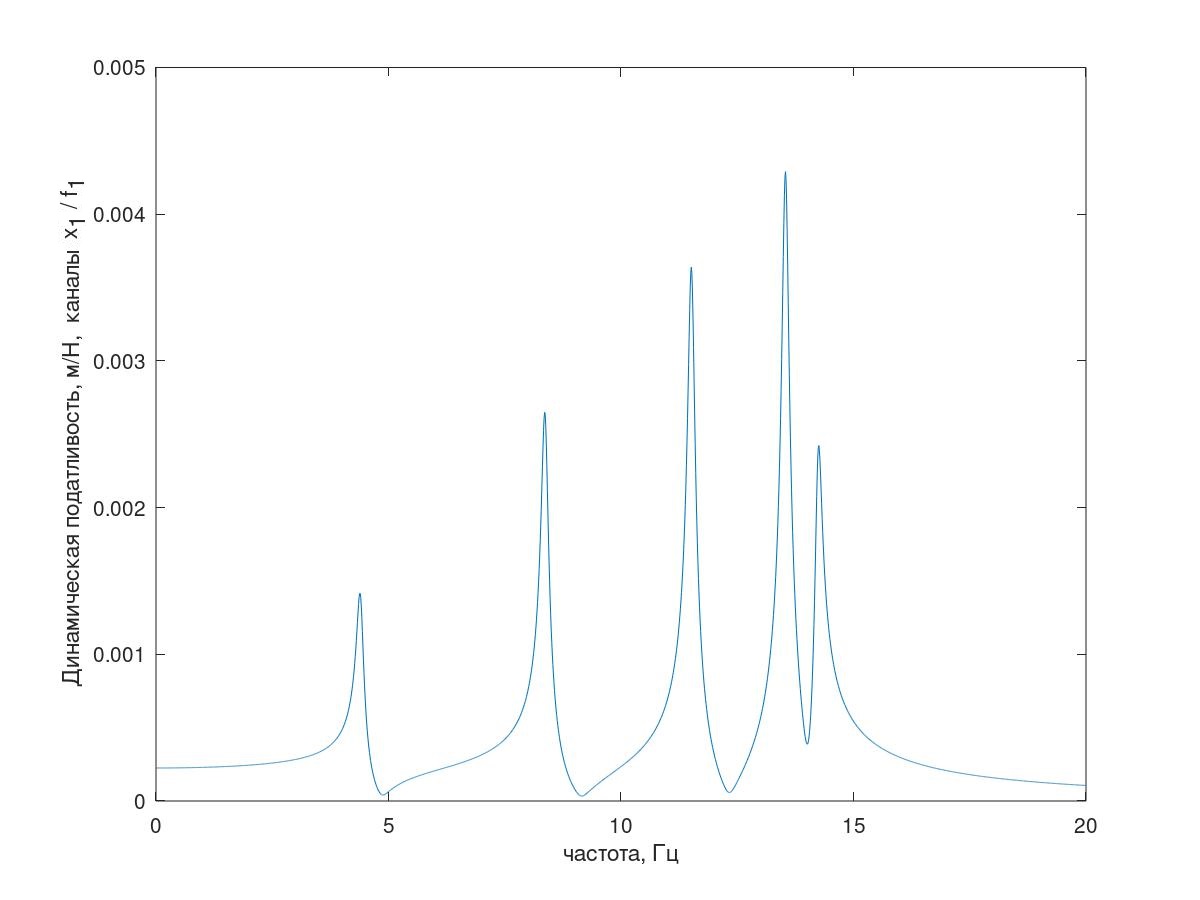 図6 5つの共振の説明。
図6 5つの共振の説明。
離散時間のシミュレーションでは、有限差分モデルが使用されます(ラマンモデル
は、示されているように 、小さなサンプリング間隔で適切に機能し
ます )。
小さな余談。 しばらくして、別の作業のフレームワークで、他の手段によるこのテストシステムの有限差分モデリングが実行されました(Xcos \ Simulink)。 数学的には、モデルは同一です。 ノードNo 1およびノードNo 3での単一インパルスに対するシステムの応答のアニメーション画像が取得されました。 この結果は、有限差分モデルの検証の観点から興味深いものです。

(フリーソフトウェアフレームの「予測不可能な」バッファリングにより、イメージ、特に2番目のイメージが多少損なわれますが、原則として結果は非常に良好です。)
しかし、Matlab(GNUOctave)モデルに戻ります。 結果の応答スペクトルを図7に示します。
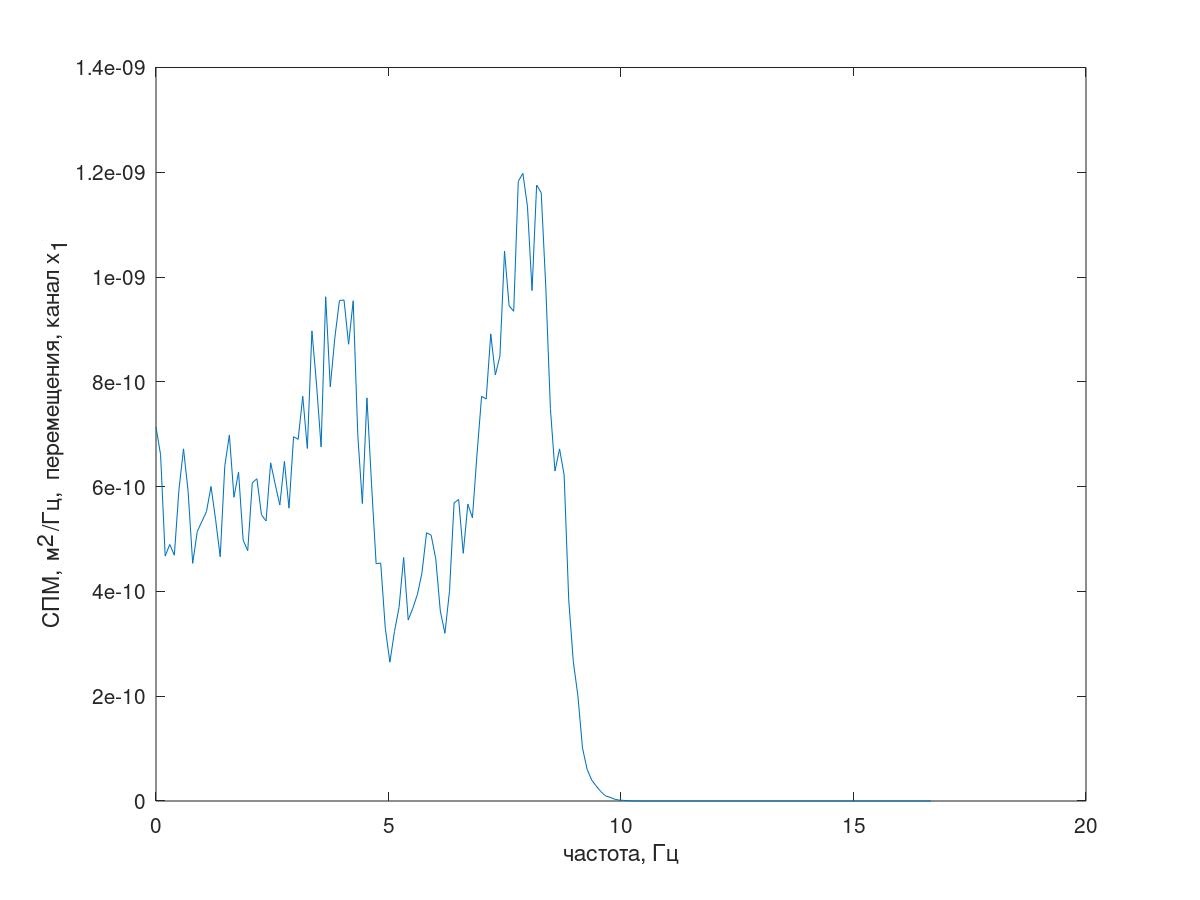 図7応答スペクトル(チャネルx 1 )
図7応答スペクトル(チャネルx 1 )次に、コレログラム法を使用して、応答チャネルの自動相関と相互相関を見つけました。
議論中の方法を適用した結果:擬似モーダルプロセスRqqの分散とH自体の擬似固有形式が見つかりました:

分解の最初の3つのプロセス、マルチチャネルプロセス全体のアニメーション、および32サンプルの対応する最初の3つの振動モード(6714から6746カウント、つまり67.13秒まで)は、明らかに(Rqqの分散の値によって)定量的に有意です67.63 s現在時刻)は、記事の冒頭の図1に示されています。 ご覧のように、これらの疑似フォームには、独自の弦振動のフォームといくつかの類似点があります。
蓄積された経験は、この方法の以下の特徴を示しています。
- この方法は、次のような外来ノイズに敏感です。 高周波。 「ランダムな」結果(ランダムエラーが大きい)を取得する危険性と、実験結果の見かけ上の再現性があります。 マルチチャネル信号の周波数範囲の非動作(定量的には重要ではない)部分を慎重に除外する必要があります。 (かつて、この方向の作業は、チャネル間の相関の「不在」に関する実験報告のために停止されました-強いノイズの影響)
- 最良の結果が得られたのは、予想される振動形態の出現数(調査範囲内の共鳴ピークの数)よりも大幅に多い観測チャネルの数、つまり m << nの場合。
- 品質係数が高いと、擬似フォームシステムはシステムの真の固有モードになりがちです。 そのようなシステムで得られた結果は、ノイズの場合により安定しています。
- 固有値のペアRxx [0]が一致するか収束する場合、対応する擬似形式のペアは、明らかに独立した線形結合まで決定されます。このような形式は、特定の実験条件下では分離できません。
- どうやら、(他の方法で見つかった)真の形式と考慮された擬似形式を比較すると、そのような問題が関連する場合、何らかの確率で外部摂動の適用点(特に小チャネル摂動)を見つけることが可能です。