IT業界の誰
もが、プロジェクトの期限
を評価する
ことがいかに
難しいかを知っています。 困難な課題
を解決するのにかかる時間を客観的に評価することは困難です。 私のお気に入りの理論の1つは、これは単なる統計上の成果物であるということです。
1週間でプロジェクトを評価するとします。 同様に3つの結果があると仮定します。それは、1/2週間、1週間、または2週間かかります。 結果の中央値は実際には推定値と同じです:1週間ですが、平均値(別名平均、別名期待値)は7/6 = 1.17週間です。 スコアは実際には中央値(1)に対して較正されます(部分的)が、平均値に対してではありません。
「インフレ率」(推定時間で割った実際の時間)の合理的なモデルは、
対数正規分布のようなものです。 推定値が1週間に等しい場合、実際の結果を約1週間の対数正規分布に従って分布したランダム変数としてシミュレートします。 このような状況では、分布の中央値は正確に1週間ですが、平均値ははるかに大きくなります。

インフレーション係数の対数を取ると、中心が約0の単純な正規分布が得られます。これは、インフレーション係数の中央値が1xであると想定しています。ご想像のとおり、log(1)= 0です。正規分布の標準偏差に対応するパラメーターσを変更することで、それらをモデル化できます。
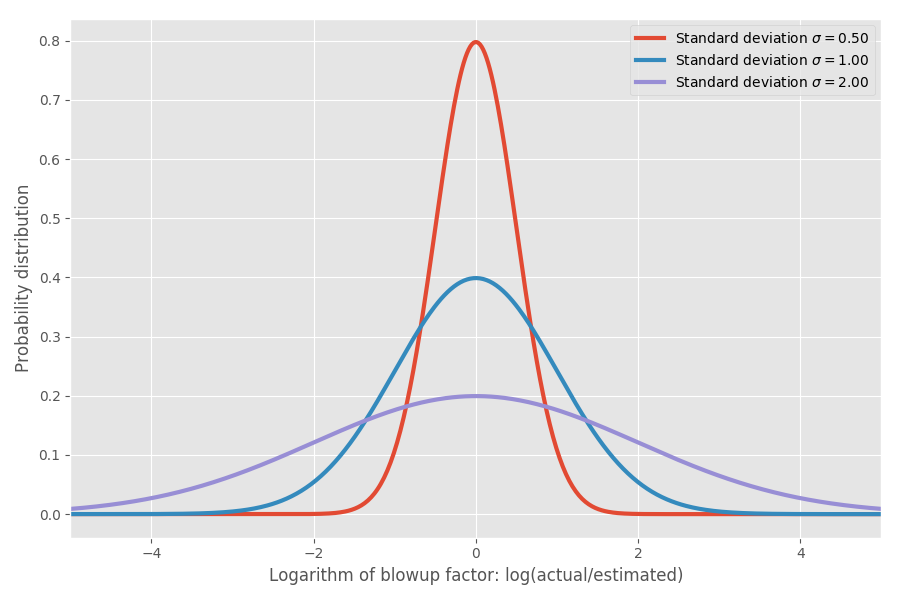
実数を表示するだけです。log(実際/推定)= 1の場合、インフレ係数exp(1)= e = 2.72です。 同様に、プロジェクトはexp(2)= 7.4倍に伸び、exp(-2)= 0.14、つまり推定時間の14%で終了する可能性があります。 直感的には、平均が非常に大きい理由は、予想よりも速く実行されるタスクは予想よりもはるかに時間がかかるタスクを補正できないためです。 0に制限されていますが、他の方向には制限されていません。
これは単なるモデルですか? できたらいいのに! しかし、すぐに実際のデータに到達し、いくつかの経験的データで、実際にそれが現実と非常によく一致していることを示します。
ソフトウェア開発タイムラインの推定
これまでのところは良いですが、実際にソフトウェア開発のスケジュールを見積もるという意味でこれが何を意味するのかを理解してみましょう。 20の異なるソフトウェアプロジェクトの計画を見て、
それらをすべて完了
するまでにかかる時間を評価しようとするとし
ます 。
ここで平均が決定的になります。 平均は合計されますが、中央値はありません。 したがって、N個のプロジェクトの合計を完了するのにどのくらい時間がかかるかを知りたい場合は、平均値を調べる必要があります。 同じσ= 1の3つの異なるプロジェクトがあるとします。
平均が合計されて4.95 = 1.65 * 3ですが、他の列はそうではないことに注意してください。
次に、異なるシグマの3つのプロジェクトを追加しましょう。
平均はまだ形をとっているが、現実はあなたが期待したかもしれない素朴な3週間の見積もりにさえ近くない。 σ= 2の非常に不確実なプロジェクトは、平均完了時間に関して残りを
支配することに注意してください。 また、99パーセンタイルでは、支配的なだけでなく、文字通り他のすべてを吸収します。 より大きな例を挙げることができます:
繰り返しますが、少なくとも99%のケースで、唯一の不快なタスクが主に推定計算を支配します。 平均的な時間であっても、1つのクレイジーなプロジェクトは、中央値が近いものの、最終的にすべてのタスクに費やされる時間の約半分を取ります。 簡単にするために、すべてのタスクの時間推定値は同じであるが、不確実性が異なると仮定しました。 条件が変更されると、数学が保存されます。
おもしろいですが、私は長い間この気持ちがありました。 多くのタスクがある場合、評価の追加はほとんど機能しません。 代わりに、どのタスクの不確実性が最も高いかを調べます。通常、これらのタスクは平均実行時間を支配します。
この図は、平均と99パーセンタイルを不確実性(σ)の関数として示しています。
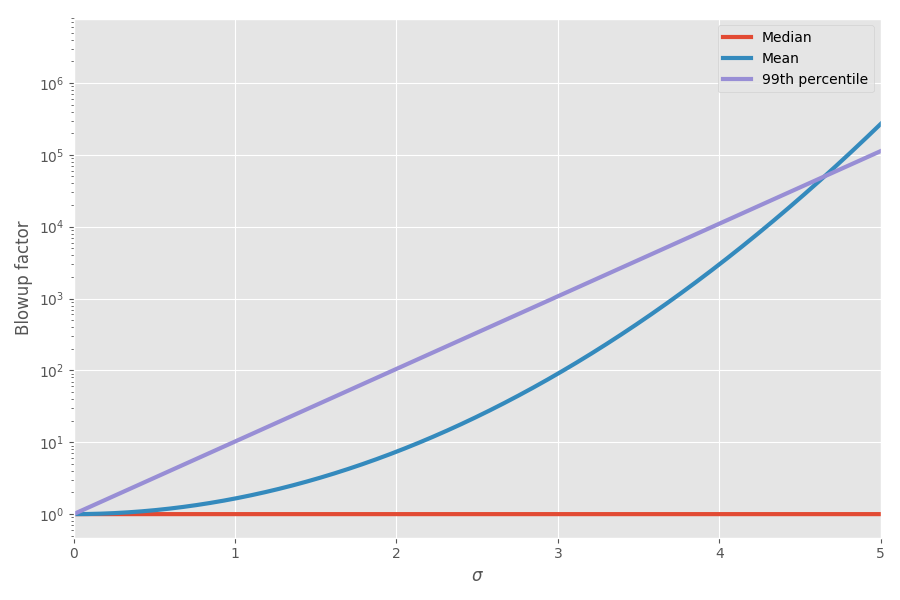
今、数学が私の感覚を説明しました! プロジェクトを計画するとき、私はこれを考慮し始めました。 タスクの締め切りの見積もりを追加することは非常に誤解を招きやすく、プロジェクト全体にかかる時間の誤ったイメージを作成すると思います。
経験的証拠はどこにありますか?
長い間、「好奇心の強いおもちゃのモデル」のセクションでそれを脳内に保管していましたが、これは実世界の現象のきちんとした説明だと時々思っていました。 しかし、ある日、ネットワークをさまよいながら、プロジェクトのタイミングとプロジェクトを完了する実際の時間を評価するための興味深いデータセットに出会いました。 フィクション!
推定時間と実際の時間の簡単な散布図を作成しましょう。
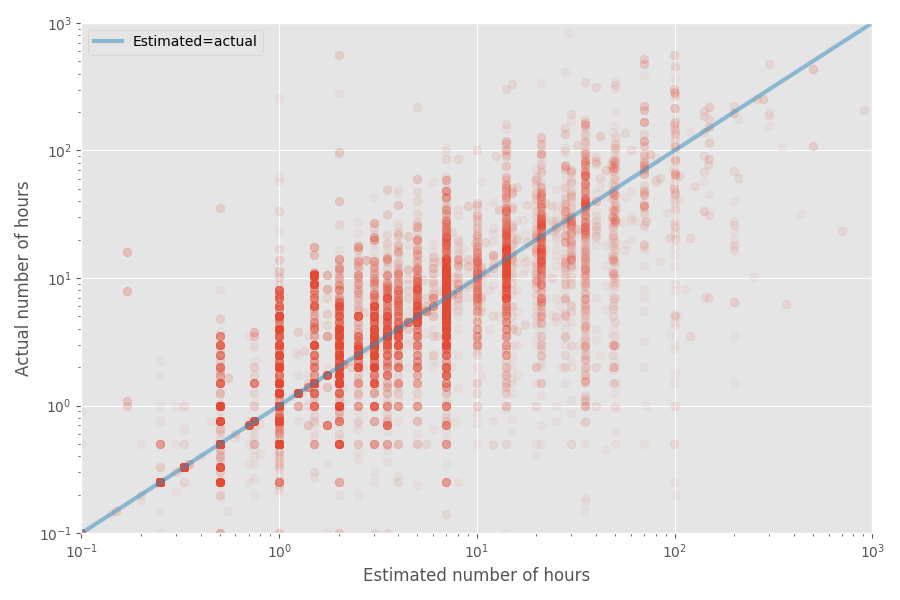
このデータセットのインフレ率の中央値は1倍であり、平均係数は1.81倍です。 繰り返しになりますが、これは開発者が中央値を適切に評価するという推測を裏付けていますが、平均ははるかに高いです。
インフレーション係数(対数)の分布を見てみましょう:
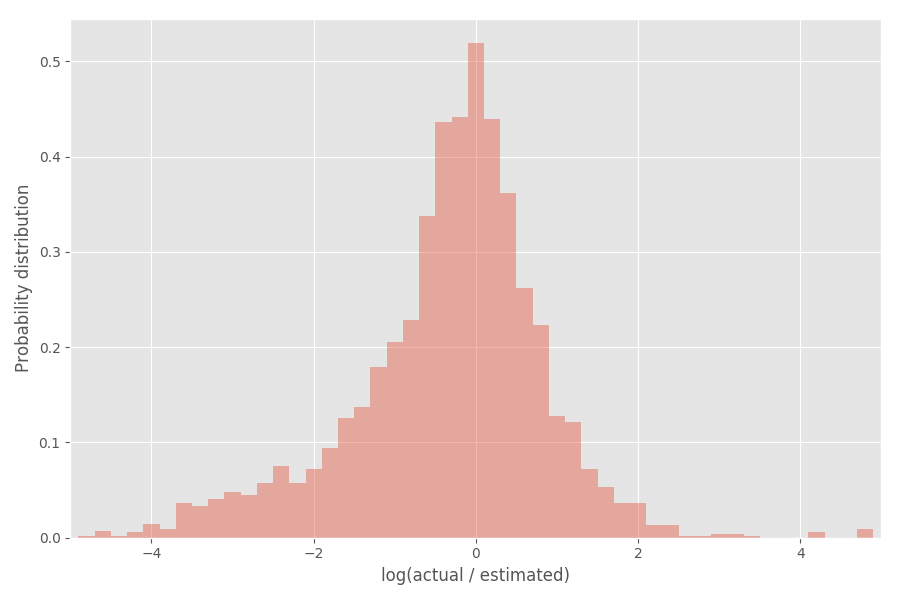
ご覧のとおり、インフレ係数exp(0)= 1の0を中心にしています。
統計ツールを取る
ここで、統計を少し空想します。興味がない場合は、この部分をスキップしてください。 この経験的分布から何を結論づけることができますか? インフレ率の対数が正規分布に従って分布することを期待できますが、これは完全に真実ではありません。 σ自体はランダムであり、プロジェクトごとに異なることに注意してください。
σをモデル化する便利な方法の1つは、
逆ガンマ分布から選択
することです。 (以前のように)インフレ係数の対数が正規分布に従って分布していると仮定すると、インフレ係数の対数の「グローバル」分布は
スチューデント分布で終わります。
学生分布を前の分布に適用します:

私の意見では、はっきりと収束します! 学生分布パラメータは、σ値の逆ガンマ分布も決定します。
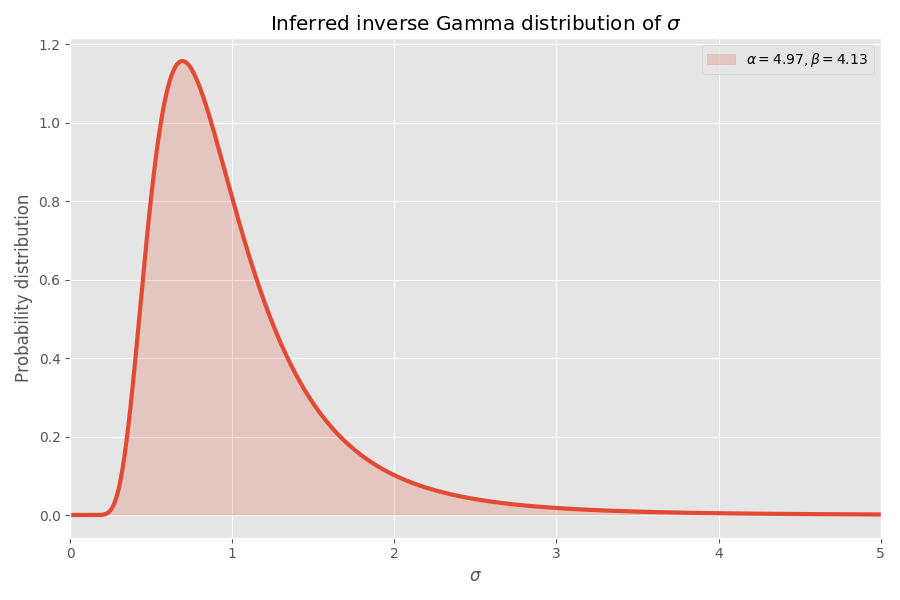
σ> 4の値はめったにありませんが、それらが発生すると、数千回の平均爆発を引き起こします。
ソフトウェアのタスクが常に思ったよりも長くかかる理由
このデータセットがソフトウェア開発の代表(疑わしい!)であると仮定すると、さらにいくつかの結論を引き出すことができます。 Student分布のパラメーターがあるため、このタスクのσを知らなくてもタスクを完了するのに必要な平均時間を計算できます。
この適合からのインフレ率の中央値は1倍(以前のように)ですが、99%のインフレ率は32倍ですが、99.99パーセンタイルにすると、なんと5500
万です! 1つの(無料の)解釈では、一部のタスクは最終的に不可能です。 実際、これらの極端なケースは
平均に非常に大きな影響を与え
、タスクの平均インフレ率は
無限になります。 これは、期限を守ろうとしている人にとってはかなり悪いニュースです!
まとめ
私のモデルが正しい場合(大きな場合)、次のようになります。
- 人々はタスクを完了するための時間の中央値をよく見積もっていますが、平均ではありません。
- 分布が歪んでいる(対数正規分布)ため、平均時間は中央値よりもはるかに長くなっています。
- n個のタスクの見積もりを追加すると、事態はさらに悪化します。
- 最大の不確実性(むしろ最大サイズ)のタスクは、多くの場合、すべてのタスクを完了するために必要な平均時間で優位に立つことができます。
- 私たちが何も知らないタスクの平均実行時間は、実際には無限です。
注釈
- 明らかに、結論は私がインターネットで見つけた1つのデータセットのみに基づいています。 他のデータセットでは異なる結果が得られる場合があります。
- もちろん、私のモデルは、統計モデルのように非常に主観的です。
- このモデルをはるかに大きなデータセットに適用して、その堅牢性を確認できれば幸いです。
- すべてのタスクが独立していることを提案しました。 実際、それらは分析をずっと厄介なものにする相関関係を持っているかもしれませんが、(私は)同様の結論に達すると思います。
- 対数正規分布値の合計は、別の対数正規分布値ではありません。 ほとんどのタスクは単にサブタスクの合計であると主張できるため、これはこの分布の弱点です。 私たちの流通が持続可能であればいいでしょう。
- ヒストグラムから小さなタスクを削除しました(推定時間は7時間以下です)。なぜなら、それらは分析を歪め、正確に7の奇妙な急増があったからです。
- コードは通常どおりGithubにあります。