こんにちは、読者の皆様！ これは、Chris Heckerによる物理エンジンの作成に関する一連の記事の2番目に翻訳された記事です。 最初のにまだ慣れていない場合は、すぐにすべてが明らかになるため、これを行うことをお勧めします。 最初の翻訳をサポートしていただき、ありがとうございます。さらに多くの作業を行うことは非常に励みになります。 素敵な読書を！

物理学、パート2、角度効果

侵入者が入らないように、何か重いものでドアを後退させたかっただけです。 私はたくさん尋ねていますか？ 私は彼の車が転がって、特定の場所で爆発してほしい。 巨大な歯車が平らになる前に固執したいです。 そして、城の要塞の壁からかわいい光る贈り物をカタパルトするために、スイングのように見えるものを急いで構築したいと思います。 これらすべてを現実に変換するのを誰が止められますか？ 対戦相手はゲームの世界にいると仮定しますが、実際には物理エンジンのプログラマーです。上記のすべてが角度効果に基づいているからです。 コーナーエフェクトが実装されているゲームを指で数えることができます。これが正しく行われているゲームを少なくとも1つ見つけることは言うまでもありません。

角度（または回転）効果が今日のゲームに実装されない主な理由は、プログラマーが回転運動を記述する物理学を理解し、現実に変換するには複雑すぎると考えているためです。 高校の物理学のクラス（私たちは全員ニュートンの第二法則を学んだ）で、彼らは通常、回転効果については語らず、オブジェクトに加えられた力からこのオブジェクトの回転に移動する方法は完全には明らかではない もちろん、回転運動のダイナミクスは直線運動のダイナミクスよりも理解するのが少し難しいですが、見た目よりも簡単です。 サイクルの最初の記事に記載されている資料に従って物理エンジンを作成できる人は、この記事で説明されている角度効果を含めることもできます。 この記事の公開後、世界はコーナー効果のすべての可能性と利点を使用するゲームで満たされるか、少なくともあなたが曲がったときに致命的な戦いで足で友達を撃つゲームを作成できることが望まれます。

短い繰り返し

いくつかのユニークなトピックに関する私の記事のそれぞれにもかかわらず、私はどこで終わったかを理解するために以前に書いたものを常に読み直しました。 私は物理学に関する最初の記事を見て、とてもうれしく思います。何とか多くのことを学べて、さらに、プログラムコードを書いたり、追加の文献を読んだりもしませんでした。 始める前に、前回の記事の資料を更新しましょう。



表1に、固体のダイナミクスに関する最も重要な結論を示します。 式1から、座標ベクトル（r）、速度ベクトル（v）、および加速度ベクトル（a）は、導関数（および逆順で読み取ると積分）によって関連付けられます。 念のため、時間の微分を素数（r '）でマークします。 r 'はdr / dtと同じであり、r' 'は2階微分と同じです。 式2から、力は線形運動量（質量と速度の積）、質量、および加速度に関連付けられます。 重心の定義は、式3から取得できます（これは、すべての質量と距離が互いにバランスをとるポイントです）。 式4では、固体の総線形運動量はそのすべての運動量の合計であり、幸運なことに、これは単に重心（CM）の運動量に等しいと述べています。 式5は本物です。 式4を使用して、スカラー量であるオブジェクトの質量を介して、オブジェクトの重心の加速度が総力（特定の時間にオブジェクトに作用するすべての力の合計のベクトル）に関連していることを示します。

最初の記事で説明されているすべてのことを要約すると、重心に作用する総力は、体に加えられるすべての力の合計に等しいことがわかりました（重力、悪役のワゴン、近くの爆発、エンジンの推力など）。 。）。 その後、CM加速度を取得するためにこの合計ベクトルを体重で除算し、時間加速度を積分して身体の速度と座標を取得しました。

式5はまさに傑作です！ その中に、体に力を加えるポイントの概念がないことがわかります。これは、体がアクションの下でどのように回転するかを決定する重要なポイントです。 式5は正しいです。 実際、直線加速度を見つけるのに最適です。 戦いの半分を逃しています。 しかし、まず最初に...

あなたの角度は？

最初の記事では、回転は無視されたため、2Dで体の構成を記述するために半径ベクトルとその導関数のみが必要でした。 次に、角効果を操作するために、別の運動学的値である方向（大文字のオメガ-Ωで表示）を追加します。 Ωを設定するには、ソリッドを基準にした座標系とゲームワールドの座標系を選択する必要があり、図1に示すように、Ωの値はラジアン単位の角度の差に等しくなります。



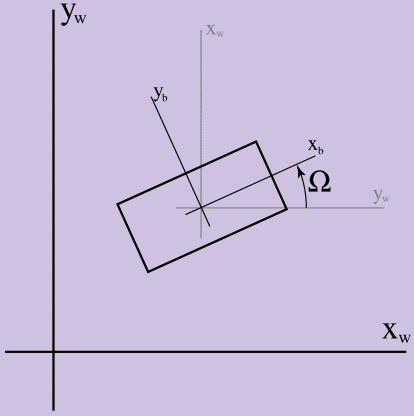図1.Ωの定義

この図では、xw、yw軸はゲームワールドの座標軸であり、xb、ybはソリッドの座標軸です。 反時計回りにカウントした場合、Ωは0より大きくなります。 ここで重要なのは、3次元に移動する前に2次元世界のダイナミクスを研究する理由を明らかにすることです：2次元の方向はスカラー量（ラジアン単位の座標系間の角度）ですが、3次元世界の方向を決定することははるかに困難です。

体が回転すると、Ωの値が変化します。 この変化は、別の運動学につながります-角速度（小文字のオメガ-ωで表されます）。 体の座標および線速度とは異なり、角速度を次のように示しません-Ω '。 ただし、時間に対する速度の微分、または角加速度をω '（これは別の運動学の値です）またはα（小文字のアルファ）で表すことがあります。 私を責めないでください。これらすべての指定を思いついたのは私ではありません。 そして、私が読んだすべての本には、わずかな矛盾があります。 式1の対応する角度は次のとおりです。

$$$$ディスプレイ$$ {d ^ 2Ω\ over {dt ^ 2}} = {dω\ over {dt}} =ω '=α$$ display $$

式6

式1のように、ωを時間で微分してαを取得します。 そして、αを経時的に積分すると、ωなどが得られます。すべて、前の記事との類推によって：αの角加速度がわかっている場合、それを2回積分して新しい方向を取得できます。 ただし、ここで重要なのは、αの値を知ることです。

ご想像のとおり、この記事の目的は、表1の各線形方程式の角度アナログを導出し、線形方程式と角度方程式、およびオブジェクトに加えられる力を考慮して、線形加速度aと角加速度αを計算することです。 最後に、これらの加速度を数値的に統合して、体の新しい位置と方向を見つけることができます。

まず、線形量と角度量を一緒に接続します。 そして、これは角速度が使用されるかなり明白なトリックです。 ダイナミクスで計算する場合、オブジェクト上の任意のポイントの速度を見つける必要があることがよくあります。 たとえば、ソリッドの衝突を計算する場合、衝突するポイントの速度を知って、衝突するポイントの量を把握する必要があります。 体が回転しない場合、体の各点の速度は同じです。 体の重心の速度を監視するだけで十分です。 一方、体が回転する場合、これらの体の各ポイントは異なる速度を持つことができます。 明らかに、剛体の無数のポイントの速度を計算することはできません。したがって、別のより良い解決策が必要です。

オブジェクト内の任意の点の線速度を見つけるために使用される簡単な方法の1つは、オブジェクトの角速度を使用します。 ボディの座標を変更せずに、ボディが1つの固定点Oを中心にのみ回転する場合を考えます。 つまり、体は回転しますが、動きません。 式7から、回転体のポイントBの速度を計算する方法に従います。

$$$$ディスプレイ$$ v ^ B =ωr^ {OB}_⟂$$ディスプレイ$$

式7

式7でいくつかの点を明確にする必要があります。これについて少し時間をかけてみましょう。 まず、トップインデックスを使用して、これらのポイントに属するパラメーターを表示します。したがって、v ^ Bは体のポイントBの速度ベクトルです。 同様に、r ^ OBは、体Oの回転中心から点Bに引かれたベクトルを示します。面白い逆文字Tは、ベクトルに作用する「垂直演算子」であり（式7のベクトルrのように）、反時計回りに90度回転します矢印。 つまり、古いベクトルに垂直な新しいベクトルが作成されます。 2次元の世界では、（x、y）に垂直なベクトルはちょうど（-y、x）です。 私の言葉はグラフ用紙で簡単に確認できます。 これについてもっと話しましょう。 垂直ベクトルの大きさは角速度ωによって決定され、線速度v ^ Bを設定します。 ロシア語では、式7は、回転体の点の速度が、回転中心から引き出された垂直ベクトルに角速度を掛けることによって計算されることを示しています。 どうすればそれを理解できますか？ まあ、私は本でそれについて読んだが、そのような説明が十分ではないことは明らかなので、これが真実であることを証明する。

式7の結論の真理を2段階で証明しましょう。 まず、結果の速度ベクトルの値が正しいことを証明します。 その後-彼の方向が正しいこと。 証明の最初の部分については、図2を検討してください。



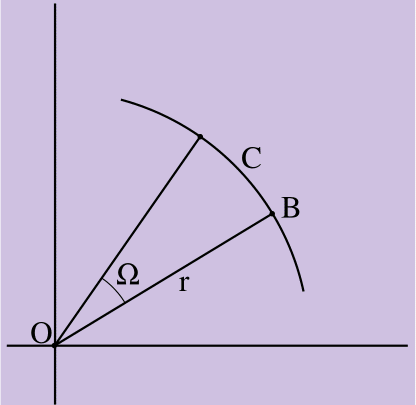図2. C =Ωr

図2は、物体Oの回転中心から点Bに向けられた長さrの半径ベクトルを持つ剛体の回転に沿ったΩラジアンに等しい角度による点Bの回転を示しています。Bは弧Cの長さを通過しました。 （角度のラジアン測度は、円の半径で囲まれた弧の測度です。円の弧のラジアン測度は2π[または360度]であるため、円周はC =2πrです）。

ポイントの速度は、時間の座標の変化です。 したがって、時間に関して運動方程式を微分することにより、ポイントBの速度、つまり速度ベクトルの大きさを見つけることができます。 C =Ωrは運動方程式です。

$$

$${d（Ωr）\ over {dt}} = {dΩ\ over {dt}} r =ωr$$

半径は微分記号から取り出されます。これは定数であるため（ポイントBは線形変位なしで単純に回転します）、時間微分Ωは式6のωです。したがって、ベクトルBの大きさは速度ベクトルωrです。

式7を考慮すると、垂直線はベクトルの長さに影響せず、r ^ OBはOからBに向けられた半径ベクトルであるため、速度ベクトルの大きさが正しいことがわかります。

式7の速度ベクトルの方向が正しいことを確認するために、速度ベクトルが半径ベクトルに垂直でなければならないことを確認することから始めましょう。 この仮定は直感的に理解できます。これは、他の特定のポイントを中心に回転するポイントは、これらのポイント間のベクトルに対して垂直にしか移動できないためです。 回転の中心に近づいたり、そこから離れたりすることはできません。または、この動きは単に回転をやめるだけです。 ベクトルの計算で仮定をサポートすることはできますが、記事のボリュームの特定のフレームワークに限定されているため、仮定が正しいと仮定します。 （自分でこれを証明したい場合は、固定長ベクトルのスカラー積をそれ自体で微分してください。）

最後に、図は半径に垂直な等しい長さの2つのベクトルvと-vを示しているため、ベクトルが正しくマークされていることを確認する必要があります。 Ωの値は反時計回りに測定されるため、ポイントが時計回りに回転するとω> 0になります。 垂直は、半径ベクトルのような時計回りの方向を指します。 図3は、式7の結論を示しています。



図3.線速度と角度の関係

式7を補足して、移動体の回転を記述します。 剛体の運動は、身体の回転中心の単純な動きと、この点を中心とした身体の残りの単純な回転と見なされます。 興味のある人にとって、これは動きの分類に関するShalの定理です。

Challの定理は、モーションを2つのコンポーネント（線形と角度）に分割します。 物体Oの回転中心を唯一の移動点とし、ωを使用して点Oの周りの回転を計算すると、式7の一般形式が得られます。

$$$$表示$$ v ^ B = v ^ O +ωr^ {OB}_⟂$$表示$$

式9

式9は、体の回転中心の直線速度と、さらに体の回転中に取得した速度を使用して、動体の任意の点の速度を計算できることを示しています。

衝動の理由

これで、力の方程式である方程式2の角度の類似物を書くことができます。 別のポイントAの周りの特定のポイントBの角運動量L ^ ABを決定することから始めます。

$$

$${L} ^ {AB} = {\ vec r} ^ {AB} \回{\ vec p} ^ B$$

式10

点の運動量は、方程式の角度バージョンが空間内の物体の位置を考慮するという点で、点の線形運動量とは異なります。 このことから、特定のポイント（その質量と速度の積）に対して決定される線形インパルスとは対照的に、ゲームワールドの異なる場所でポイントの角運動量を測定する必要があります。 これは、式10の上側のインデックスによって示されます。エントリL ^ ABは、角運動量が点A（体の回転中心）から点Bに対して測定されることを示しています。 ポイントAからポイントBを指す矢印を想像してください。この矢印は2つのポイント間の半径ベクトルであり、r ^ ABを意味します。 したがって、点の角運動量は、線形運動量ベクトルとそれに垂直な半径ベクトルのスカラー積です。 この操作は「垂直のスカラー積」と呼ばれ、3Dベクトル積の2Dアナログですが、これについては後で説明します。

式10の結果を図4で説明したように紙上で図式化すると、点Bの線形モーメントがAを「回転」する方法の尺度を決定することがわかります。



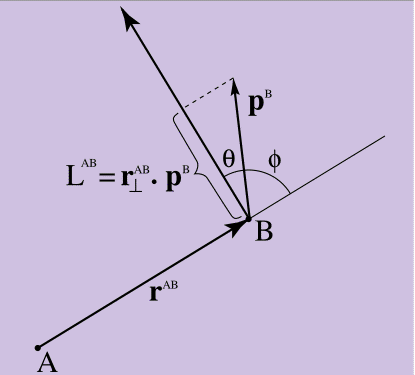図4.衝動の瞬間

ポイントBの運動量がポイントAを直接指す場合、式10 = 0（rに対する垂線がpと直角を形成し、スカラー積が0になるため）はすべて正しいです。 Aに垂直に向けられた運動量Bが大きいほど、運動量は大きくなります。 図4からわかるように、式10のスカラー積は、パラメーターとして、垂直r ^ ABからp ^ Bに囲まれた角度θの余弦を持ちます。 一方、スカラー積の大きさは、垂直r ^ ABとp ^ Bではなく、元の角度φのサインによって与えられます（サインは、ベクトルとスカラー積の関係を解明するためのもう1つの鍵です）。 式10は、ポイントBの運動量がポイントAに対して「回転方向」にどれだけ「見える」かを示します。

また、力を決定するために線形運動量の導関数を使用したため、角運動量の導関数を使用して、力の角双子-力のモーメント（小文字tau-τで示される）を決定します。

$$

$$τ^ {AB} = {dL ^ {AB} \ over dt} = {d（{\ vec r} ^ {AB} \ times {\ vec p} ^ B）\ over dt} = \ vec r ^ { AB} \回ma ^ B = \ vec r ^ {AB} \回F ^ B$$

式11

スペースを節約するために、導関数の検索を含むいくつかの難しいステップをスキップして、式11で少しごまかしました。 上記から、力のモーメントは、スカラー積を介して特定の点での力に関連付けられることがわかります。

最後に、力の適用点を使用する動的方程式を得ました。これは、以前は線形運動量方程式では無視されていました。 式11は、ポイントBに加えられた力がポイントAを中心に回転する度合いの尺度として、垂線をもつスカラー積を使用します。 この「回転力」は、力のモーメントと呼ばれます。 式11を使用すると、力のモーメントの数値、つまり力のモーメントを積分し、加えられた力と作用点を知ると角運動量を見つけることができます。

ただし、角運動量と、角加速度、角速度、向きなど、オブジェクトをその軸の周りに回転させるために必要な角運動学との関係の方程式はまだ受け取っていません。 したがって、さらにいくつかの方程式を導き出すまでは前進できません。

みんな待っていた瞬間

ダイナミクスとキネマティックスを接続する前に、式4で総線形運動量を決定した方法と同様に、総角運動量を決定する必要があります。式3で重心の等価角を忘れていません。 全角運動量の方程式でそれを見ることができます。

点A付近の全角運動量はL ^ ATで表され、式12で決定されます。

$$

$$L ^ {AT} = {\ sum _ {i} {} {\ vec r ^ {Ai} \ times p ^ i}} = {\ sum _ {i} {\ vec r ^ {Ai} \ times m ^ iv ^ i}}$$

式12

式12は、体のすべての点のすべての角運動量の合計であり、点Aに対して測定されます。右側では、質量と速度（mv）の積としてp ^ iを表すために線形運動量の定義を使用しました。 これは、式12からより明確に適用された特性を持つ何かを作成するために、将来的に私にとって有用です。 方程式は、オブジェクトの総角運動量を見つけるには、そのすべての点の角運動量を合計する必要があることを示しています。 （個別の点からではなく）面で構成されるソリッドボディの場合、非離散和の積分を計算する必要があります。

幸いなことに、「慣性モーメント」と呼ばれる新しい量を導入することで計算を簡素化できます。これは、総運動量方程式を単純化するために重心を導入した方法と同様です。 式7のおかげで、角速度でポイントの速度を見つけることができることを思い出してください。 式12の点Aが式7の回転中心であり、式12の加算インデックスiが式7の点Bであると仮定すると、式7を式12に変換できます。

$$$$表示$$ L ^ {AT} = \ sum _ {i} {\ vec r ^ {Ai} \ times m ^ iω\ vec r ^ {Ai}} =ω{\ sum _ {i} {m ^ i \ vec r ^ {Ai} \ times \ vec r ^ {Ai}}} =ω\ sum_ {i} {m ^ i（\ vec r ^ {Ai}）^ 2} =ωI^ A $$ディスプレイ$$

式13

式13をステップごとに詳しく説明します。 最初に式13の合計を得るために式7を12に置き換えます。この置き換えにより、角速度を使用して角運動量を記述できます。 次に、合計のωを取得します。これは、ソリッドのすべてのポイントで等しいため（角速度は各ポイントで個別にではなく、全身全体で決定されます）、スカラー積半径をより明確に見るために、左側にインデックスiを持つ質量を書き留めます自身のためのベクトル。 このスカラー積は、半径ベクトルの長さの2乗に等しくなります（ベクトル自体のスカラー積=それ自体の長さの2乗。垂直演算子はベクトルの長さを変更しないことに注意してください）。 最後に、点Aの周りの慣性モーメントを示すためにI ^ Aを書きます。

2次元の立体の慣性モーメントは、身体を構成するポイントが質量を変更したり、回転の中心から離れたりできないため、非常に良い数値です。 これらの2つのプロパティの結果として、式13の合計は各ボディの定数なので、計算できます。 ロシア語では、I ^ Aは、ポイントAから体内の他のすべてのポイントまでの距離の2乗の合計であり、そのような各距離は各ポイントの質量に応じてスケーリングされます。 ちょうど重心のように-体が離散点で構成されるよりも固体である場合、合計は積分に変わります。 そして、慣性モーメントの大きさは同じままで、同じ物理的意味を持ちます。

ポイント付近の慣性モーメントの決定は冗長ですが、I ^ Aは、ポイントAを中心に身体を回転させるのがどれだけ難しいかの尺度と考えてください。たとえば、鉛筆（フラットペンシル）を想像してください。 鉛筆の中心付近の慣性モーメントを測定すると、各ポイントの質量に応じてスケーリングされた距離の二乗和に等しい特定の値が得られます。 一方、同じ鉛筆の先端で慣性を測定すると、質量のあるポイントが削除されるほど、距離の2乗の値が大きくなるため、より大きな値が得られます。 ここでは、直感的に理解できるものを数学的に定式化します。鉛筆を中心の周りで回転させるのは、端の1つで回転させるよりもはるかに簡単です（読みやすくなります）。

最後に、ダイナミクスの角方程式と運動学の角方程式の間の関係を描く準備ができました。 式13を微分すると、左に総力モーメント、右に慣性モーメントと角加速度の積が得られます（I ^ Aは定数です。微分の符号の外側に置きます）。

$$$$ディスプレイ$$τ^ {AT} = {dL ^ {AT} \ over dt} = {d（I ^ Aω）\ over dt} = I ^ Aω= I ^ Aα$$ディスプレイ$$

式14

この式は、式5と同等の角度です。 実際、角ダイナミクスではF = maです。 これは、力の総モーメントとスカラー慣性モーメントによる身体の角加速度の関係の方程式です。 体にかかる力のモーメントがわかれば、その角加速度を見つけることができます。次に、積分により、力のモーメントを慣性モーメントで除算して、角速度と空間の向きを見つけることができます。

ダイナミクスアルゴリズム

彼は、この方程式の旋風を通して私たちを見ることはほとんどありませんが、それらはすべてその不可欠な部分です。 任意に与えられた力とオブジェクトの動きと回転の力のモーメントで、2次元の世界の壮大なダイナミクスを得るのに十分な方程式を導き出しました。 これらの方程式の使用方法は？ 基本的なアルゴリズムは次のとおりです。

1. 重心の値と重心の慣性モーメントを見つけます。
2. ボディの初期座標、空間での方向、線形および角速度を設定します。
3. 身体に作用するすべての力とその適用のポイントを考慮に入れてください。
4. すべての力の合力を求め、それを体の質量で除算して、重心の線形加速度を求めます（式5）。
5. 各力に対して、重心から力の作用点に向けられたベクトルと力の作用ベクトルとの間に垂線をもつスカラー積を作成し、この量を重心方程式の式（式11）の力の合計モーメントに追加します。
6. 角加速度を求めるために、重心の総力モーメントと慣性モーメントの商を求めます（式14）。
7. 線形加速度と角加速度を数値的に統合して、座標、線形速度、空間方向、角速度を更新します（最後の記事を参照）。
8. 結果の座標でオブジェクトを描画し、ステップ3に進みます。

上記のアルゴリズムでは、説明していない2つのステップのみがあります。 まず、ステップ1で固体オブジェクトの慣性モーメントを計算する方法は？ 第二に、ステップ3の力で問題を解決する方法は？ 最初の質問に対する答えは、この記事の最後にアプリケーションに残しておく単純なコード例にあります（オブジェクトをその領域ごとに統合します）。 ダイナミクスに関する多くの本には、アプリケーションで頻繁に遭遇するオブジェクトの最後に計算された慣性モーメントが含まれているため、毎回自分で表示する必要はありません。

ステップ3の力の計算方法の質問に対する答えはアプリケーションによって異なりますが、一般的な推奨事項をいくつか示します。 まず、重力などの力は常に一方向（重力の場合は下向き）に向けられますが、力のモーメントは発生しません。これは、すべてのポイントを同時に同じ方向に引くためです。これらの力を直接重心に加えます。 弾性力に類似した力がオブジェクトの特定のポイントに適用され、それらは力のモーメントを作成します。したがって、一般的な場合にそれらを考慮します。 最初の記事で見たように、摩擦の力は、体の速度と反対の方向に向けられた同じ力です。

摩擦の力を示す単純な物理モデルを作成し、質量の中心に力を加えるか、オブジェクトのどの部分が摩擦力を適用するかを選択して、これを行うと、オブジェクトに作用する力のモーメントを作成できます。衝突で身体が受ける力はもう少し難しく、次の記事でそれらを知ることになります。ロケットエンジンの推力のような力は、アプリケーションポイントを持つ力と見なされる必要があります（この場合、エンジンの1つが故障すると、ハンドルを調整して力のモーメントのバランスをとるまで、軸の周りを回転し始めます！） UFOからの重力光線のようなものが必要な場合は、この力を重力の力として計算し、力のモーメントを作成しないか、オブジェクトの特定のポイントに適用する必要があります。そして、上昇しながらこの点を中心に展開しますか？選択はあなた次第です。重要な点は、さまざまな方法で計算されたさまざまな力を実験することを恐れないことです。2次元グラフィックスの実際のシミュレータができたので、さまざまな種類の力を試してください。

残りのスペースがないため、必要なすべてのコードとリンクをWebサイトに残しました。単純なアプリケーションでは、2次元の世界のダイナミクスのアルゴリズムを実装し、バネで固定されたオブジェクトも追加しました。それらは軸を中心に回転し、時には壁と衝突し、回転します。しかし、私はこのことについてもう一度話します。より多くの文献とWindows 32およびMacintosh用の簡単なアプリケーションのリンクをたどってください。

クリス・ヘッカーが慣性モーメントの影響を受けることは非常にまれですが、通常は非常に速く通過します。強制はchecker@bix.comに適用できます。

翻訳者のメモ：しゃれがここに表示され、記事のトピックとその内容が表示されます。

PSフィードバックは大歓迎です。あなたのコメントは仕事の質を向上させることができます。よろしくお願いします！

PPS翻訳の著者は、翻訳を編集してくれたberezとVasily Tereshkovのユーザーに特別な感謝を表明します。よろしくお願いします！