階層的なデータ構造とパフォーマンス

はじめに

前回の記事で、リレーショナルデータベースに階層構造を格納するための基本モデルの概要を説明しました。 当然のことながら、多くの読者が、提示されたアルゴリズムのパフォーマンスについての鋭い質問になっています。

この記事では、この書き込みの問題についてのベールを開き、最適化の問題と非標準のソリューションの検索に触れることを約束します。

準備する

だから、テスト。 他のテストと同様に、私たちのテストでも、目標とアクションプランを準備、分析、開発するための特定のアクションが必要です。

実際、目標は、さまざまなデータ量でさまざまなアルゴリズムの一連のストレステストを実施することです。 また、いくつかの異なるハードウェアプラットフォームでテストを実行するのも良いでしょうが、残念ながら、著者はそれを行うことができません（時間とお金のせいです）。

当然、最も重要で重要な操作のテストを実施することは良いことです。これは通常、特定のツリーで実行されます。 非常に多くのことを考えた後、テスト済みの操作の次のリストを詳しく調べることにしました。

1. ツリー全体の選択
2. 特定のノードへのパスを取得する
3. 特定のノードのブランチ選択
4. 指定されたノードの親を検索します
5. 特定のノードの相続人を検索する
6. 指定した親ノードの最後に新しいノードを追加します
7. ノードの移動（つまり、親の変更）
8. ノード（およびその下のブランチ全体）の削除

これらの作戦を戦闘条件に近づけることは注目に値します。 入力はノードとその親の識別子になります。 これにより、各アルゴリズムの特定の実装に縛られることがなくなります。

さらに、純粋なSQLのパフォーマンスに関心があることを規定しているため、その操作のみを測定します。

著者は、操作の完全なリストであると主張していません。 おそらく誰かがノードの近隣を検索したり、ツリーのすべてのリーフを選択したり、特定のブランチ内であっても、この実験を拡張および補足する権利を持っていることを思い出してください。 それまでは、基本的な、私の意見では、基本的な最小限の機能に焦点を当てます。

ここで、関数自体の実装についてさらに詳しく説明したいと思います。テストは将来実行されます。 しかし、もしあなたが裸の数字と事実だけに興味があるなら、あなたは記事の次のセクションに進むことができます。

宣言された関数のすべてが、異なるメソッド、特に純粋なSQLで簡単な解決策を持っているわけではありません。 たとえば、ALツリーでブランチを選択することは、純粋に再帰的なタスクです。 しかし、SQLレベルでこれを行う価値はありますか？..

一般に、次の点を考慮する必要があります。

-テストが実行されるDBMS-MySQLバージョン5.0.x。 エンジンはInnoDBです（データベースレベルでALツリーのカスケード操作を実装するのに便利です）。

-クエリクエリは、SQL_NO_CACHEフラグを使用して実行され、クエリ実行の「ネット」コストを評価します。

-異なるタイプのツリーは、ノードの物理構造が同じです（つまり、1つのタイプのツリーがランダムに作成され、残りのツリーは最初から構築されます）。

-ネストセットとマテリアライズドパスのアルゴリズムは、ツリー内の現在のノードのネストレベルを格納するレベルフィールドによって強化されました。 特に、これにより、たとえばMPツリー内のノードの相続人を選択するパフォーマンスを100倍以上向上させることができます。 実際、この分野がないと、これらのアルゴリズムはある意味で魅力を失います。 したがって、このフィールドを追加する際のチューニングについてではなく、機能に必要な条件について説明します。 したがって、テストベースの構造は次のとおりです。

-- Adjacency List Tree Structure
CREATE TABLE `al_tree` (
`id` bigint(20) NOT NULL auto_increment,
`parent_id` bigint(20) default NULL ,
`name` varchar (50) NOT NULL ,
PRIMARY KEY (`id`),
KEY `fk_tree_tree` (`parent_id`),
CONSTRAINT `fk_tree_tree` FOREIGN KEY (`parent_id`) REFERENCES `al_tree` (`id`) ON DELETE CASCADE ON UPDATE CASCADE
) ENGINE=InnoDB DEFAULT CHARSET=utf8

-- Nested Set Tree Structure
CREATE TABLE `ns_tree` (
`id` bigint(20) NOT NULL auto_increment,
`name` varchar (50) NOT NULL ,
`lft` bigint(20) NOT NULL ,
`rgt` bigint(20) NOT NULL ,
` level ` bigint(20) NOT NULL ,
PRIMARY KEY (`id`),
KEY `nslrl_idx` (`lft`,`rgt`,` level `)
) ENGINE=InnoDB DEFAULT CHARSET=utf8

-- Materialized Path Tree Structure
CREATE TABLE `mp_tree` (
`id` bigint(20) NOT NULL auto_increment,
`name` varchar (50) NOT NULL ,
` path ` varchar (100) NOT NULL ,
` level ` int (11) NOT NULL ,
PRIMARY KEY (`id`),
KEY `mpp_idx` (` path `)
) ENGINE=InnoDB DEFAULT CHARSET=utf8

* This source code was highlighted with Source Code Highlighter .

-ネストされたセットツリーとマテリアライズドパスツリーを使用するために、関数とプロシージャはデータベースレベルで記述され、ツリーを使用した日常的な操作を簡素化しました。 特に、関数STRFIND、REPLACE_PATH、およびプロシージャMOVE_NODE_NS、MOVE_NODE_MP、REMOVE_NODE_MPが追加されました。

STRFIND（str、delimtr）

--
-- delimtr str.
--
-- MATERIALIZED PATH.
-- (- )
--
-- @param str VARCHAR(255) -
-- @param delimtr CHAR(1) -
-- @return INT - -
--
CREATE FUNCTION `STRFIND`(str VARCHAR (255), delimtr CHAR (1)) RETURNS INT
BEGIN
DECLARE _cnt INT ;
DECLARE _start INT ;
SET _cnt = -1;
SET _start = 1;
WHILE _start > 0 DO
SET _start = LOCATE( delimtr, str);
SET str = SUBSTRING ( str, _start + 1);
SET _cnt = _cnt + 1;
END WHILE ;
RETURN _cnt;
END

* This source code was highlighted with Source Code Highlighter .

REPLACE_PATH（_str、_match、_replace）

--
-- _str
-- _match _replace,.
-- _match _str
--
-- MATERIALIZED PATH .
--
-- @param _str VARCHAR(255) -
-- @param _match VARCHAR(255) -
-- @param _replace VARCHAR(255) -
-- @return VARCHAR(255) -
--
CREATE FUNCTION `REPLACE_PATH`( _str VARCHAR (255), _match VARCHAR (255), _replace VARCHAR (255)) RETURNS VARCHAR (255)
BEGIN
IF _str LIKE CONCAT(_match, '%' ) THEN
RETURN CONCAT( _replace, SUBSTRING ( _str, LENGTH(_match)+1, LENGTH(_str)));
END IF ;
RETURN _str;
END

* This source code was highlighted with Source Code Highlighter .

指定された関数と組み込みのREPLACEの主な違いは、行の最初から一致が見つかった場合にのみ指定された行を変更し、一度だけ変更を行うことが保証されることです。

MOVE_NODE_NS（node_id、parent_id）

--
-- NESTED SET
--
-- @param node_id - ,
-- @param parent_id -
--
CREATE PROCEDURE MOVE_NODE_NS( node_id BIGINT, parent_id BIGINT)
BEGIN
DECLARE done INT DEFAULT 0;
DECLARE c_id, c_lft, c_rgt, c_lvl, nWidth, nLeft, nRight, dtKey, nLvl, pRight, addLvl, addKey BIGINT;
DECLARE c_name VARCHAR (50);

-- ,
--
DECLARE mvBranch CURSOR FOR
SELECT id, name, lft - dtKey, rgt - dtKey, level - nLvl FROM ns_tree
WHERE lft >= nLeft AND rgt <= nRight;

DECLARE CONTINUE HANDLER FOR NOT FOUND SET done = 1;

--
SELECT rgt - lft + 1, lft, rgt, lft - 1, level INTO nWidth, nLeft, nRight, dtKey, nLvl
FROM ns_tree WHERE id = node_id;

--
OPEN mvBranch;

--
DELETE FROM ns_tree WHERE lft BETWEEN nLeft AND nRight;

--
UPDATE ns_tree SET rgt = rgt - nWidth WHERE rgt > nRight;
UPDATE ns_tree SET lft = lft - nWidth WHERE lft > nRight;

--
SELECT rgt, level + 1 INTO pRight, addLvl FROM ns_tree WHERE id = parent_id;

SELECT MAX (node.rgt) INTO addKey FROM ns_tree node, ns_tree parent
WHERE node.lft BETWEEN parent.lft AND parent.rgt AND node. level = parent. level + 1 AND parent.id = parent_id;

-- ,
--
UPDATE ns_tree SET rgt = rgt + nWidth WHERE rgt >= pRight;
UPDATE ns_tree SET lft = lft + nWidth WHERE lft > pRight;

-- .
--
REPEAT
FETCH mvBranch INTO c_id, c_name, c_lft, c_rgt, c_lvl;
IF NOT done THEN
INSERT INTO ns_tree VALUES (c_id, c_name, c_lft + addKey, c_rgt + addKey, c_lvl + addLvl);
END IF ;
UNTIL done END REPEAT;

CLOSE mvBranch;
END

* This source code was highlighted with Source Code Highlighter .

MOVE_NODE_MP（node_id、parent_id）

--
-- MATERIALIZED PATH
--
-- @param node_id - ,
-- @param parent_id -
--
CREATE PROCEDURE MOVE_NODE_MP( node_id BIGINT, parent_id BIGINT)
BEGIN
DECLARE done, m_cnt, m_rows, p_cnt, p_rows INT DEFAULT 0;
DECLARE c_id, p_id, n_pos, n_lvl, np_id, np_lvl, new_pos, dt_lvl, ch_id, ch_pos BIGINT;
DECLARE c_path, p_path, n_path, np_path, ch_path, new_path VARCHAR (100);

-- , ,
--
DECLARE mvBranch CURSOR FOR
SELECT SQL_CALC_FOUND_ROWS node.id, node. path FROM mp_tree node, mp_tree parent
WHERE node. path LIKE CONCAT(parent. path , '%' ) AND parent.id = node_id;

-- ,
-- ,
DECLARE pChildren CURSOR FOR
SELECT SQL_CALC_FOUND_ROWS node.id, node. path ,
CAST ( SUBSTRING (REVERSE(node. path ), 1, LOCATE( '.' , node. path )-1) AS UNSIGNED) as pos
FROM mp_tree node, mp_tree parent
WHERE node. path LIKE CONCAT(parent. path , '%' ) AND node. level = parent. level + 1
AND CAST ( SUBSTRING (REVERSE(node. path ), 1, LOCATE( '.' , node. path )-1) AS UNSIGNED) > n_pos
AND parent.id = p_id
ORDER BY pos;

DECLARE CONTINUE HANDLER FOR NOT FOUND SET done = 1;

--
SELECT path , CAST ( SUBSTRING (REVERSE( path ), 1, LOCATE( '.' , path )-1) AS UNSIGNED), level INTO n_path, n_pos, n_lvl FROM mp_tree
WHERE id = node_id;

SELECT parent.id, parent. path INTO p_id, p_path FROM mp_tree node, mp_tree parent
WHERE parent. path = SUBSTRING ( node. path , 1, (LENGTH(node. path ) - LOCATE( '.' , REVERSE(node. path ))))
AND node.id = node_id;

SELECT id, path , level INTO np_id, np_path, np_lvl FROM mp_tree WHERE id = parent_id;

--
-- :
SET dt_lvl = np_lvl - n_lvl + 1;

SELECT MAX ( CAST ( SUBSTRING (REVERSE(node. path ), 1, LOCATE( '.' , node. path )-1) AS UNSIGNED)) + 1
INTO new_pos FROM mp_tree node, mp_tree parent WHERE node. path LIKE CONCAT(parent. path , '%' )
AND node. level = parent. level + 1 AND parent.id = parent_id;

--
OPEN mvBranch;
SELECT FOUND_ROWS() INTO m_rows;

WHILE m_cnt < m_rows DO
FETCH mvBranch INTO c_id, c_path;
UPDATE mp_tree
SET path = REPLACE_PATH( path , n_path, CONCAT(np_path, '.' , new_pos)), level = level + dt_lvl WHERE id = c_id;
SET m_cnt = m_cnt + 1;
END WHILE ;
CLOSE mvBranch;

-- .
--
OPEN pChildren;
SELECT FOUND_ROWS() INTO p_rows;

WHILE p_cnt < p_rows DO
FETCH pChildren INTO ch_id, ch_path, ch_pos;
UPDATE mp_tree SET path = REPLACE_PATH( path , ch_path, CONCAT(p_path, '.' , ch_pos - 1)) WHERE path LIKE CONCAT( ch_path, '%' );
SET p_cnt = p_cnt + 1;
END WHILE ;
CLOSE pChildren;
END

* This source code was highlighted with Source Code Highlighter .

REMOVE_NODE_MP（node_id）

--
-- MATERIALIZED PATH
--
-- @param node_id - ,
--
CREATE PROCEDURE REMOVE_NODE_MP( node_id BIGINT)
BEGIN
DECLARE n_pos, ch_id, p_id, ch_pos BIGINT;
DECLARE n_path, ch_path, p_path VARCHAR (100);
DECLARE done, p_cnt, p_rows INT DEFAULT 0;

-- ,
-- ,
DECLARE pChildren CURSOR FOR
SELECT SQL_CALC_FOUND_ROWS node.id, node. path ,
CAST ( SUBSTRING (REVERSE(node. path ), 1, LOCATE( '.' , node. path )-1) AS UNSIGNED) as pos
FROM mp_tree node, mp_tree parent
WHERE node. path LIKE CONCAT(parent. path , '%' ) AND node. level = parent. level + 1
AND CAST ( SUBSTRING (REVERSE(node. path ), 1, LOCATE( '.' , node. path )-1) AS UNSIGNED) > n_pos
AND parent.id = p_id
ORDER BY pos;

DECLARE CONTINUE HANDLER FOR NOT FOUND SET done = 1;

--
SELECT path , CAST ( SUBSTRING (REVERSE( path ), 1, LOCATE( '.' , path )-1) AS UNSIGNED) INTO n_path, n_pos FROM mp_tree
WHERE id = node_id;

SELECT parent.id, parent. path INTO p_id, p_path FROM mp_tree node, mp_tree parent
WHERE parent. path = SUBSTRING ( node. path , 1, (LENGTH(node. path ) - LOCATE( '.' , REVERSE(node. path ))))
AND node.id = node_id;

--
DELETE FROM mp_tree WHERE path LIKE CONCAT( n_path, '%' );

--
OPEN pChildren;
SELECT FOUND_ROWS() INTO p_rows;

WHILE p_cnt < p_rows DO
FETCH pChildren INTO ch_id, ch_path, ch_pos;
UPDATE mp_tree SET path = REPLACE_PATH( path , ch_path, CONCAT(p_path, '.' , ch_pos - 1)) WHERE path LIKE CONCAT( ch_path, '%' );
SET p_cnt = p_cnt + 1;
END WHILE ;
CLOSE pChildren;
END

* This source code was highlighted with Source Code Highlighter .

実際、実装の微妙な点がすべて明らかになったので、ここでやめてテストの実施の質問に進んでください。

テスト中

テストは、次の構成で自己記述コンソールプログラムを使用して実行されました。

ハードウェア：

CPU：Intel®Core（TM）2 Duo CPU E7200 @ 2.53GHz 6Mb 64bit
RAM：4 Gb
HD：2 x 250Gb 7200rpm RAID 1

ソフトウェア：

OS：Debian Linux 2.6.26-1-amd64（64ビット）
PHP-CLI：5.2.6-5 with Suhosin-Patch 0.9.6.2
MySQL：5.0.51a、readline 5.2を使用したdebian-linux-gnu（x86_64）用

このデバイスは、現時点では重負荷（1日あたり約100,000のかなり単純なHTTP要求）にはほど遠いサーバーであり、そのような構成ではほとんど目立たないとしましょう。

ここからプログラムをダウンロードして、マシンでテストしてみてください（Unixライクな環境でのみ動作します）。 ダウンロードした配布パッケージのプログラムの使用方法については、README.TXTファイルに説明があります。

テスト中に、5つのツリー構成が選択されました。

• 100ノットおよびネストレベル5
• 1000ノットおよびネストレベル10
• 10,000ノットおよびネストレベル20
• 100,000ノードおよびネストレベル25
• 500,000ノードおよびネストレベル30

これらは、テストが正常に完了したツリーです。 すべてのテストは6時間未満で完了しましたが、ほとんどの場合、もちろん50万ノードのツリーで最後のテストが行​​われました。

ツリー作成アルゴリズムは、ツリー内のノードの分布の法則がほぼ次のようになるように機能します。



ここで、横軸は昇順のノードの識別子であり、縦軸は特定の識別子を持つノードのブランチ内のノードの数です。

この状況に関連して、次のテストスキームが選択されました。 サンプリングの場合、ツリーのさまざまな部分でサンプリングアルゴリズムの動作をチェックするための反復的な段階的なスキーム。 反復は次のように編成されます。

  id> 1 <10-ステップ1
 id> 10 <100-ステップ10
 id> 100 <1000-ステップ100
 id> 1000 <10000-ステップ1000
 id> 10000 <100000-ステップ10000
 id> 100000-ステップ100000 

これにより、ノードの分布の法則に対する検索および選択機能の依存関係を追跡できます。

変更機能の場合、スキームはわずかに異なります。 ほとんどのアルゴリズムの変更操作自体は非常に高価な操作であるため、それらを繰り返し確認することは意味がありません（テスト完了の待機時間が長くなりすぎます）。 したがって、検証方法は、ツリーの先頭にある最大ノードの1つに変更を加えることに基づいています。 また、このようなテストは1回実行されます。 全体像を概説し、問題の範囲を概説するには、これで十分です。

分析

したがって、テストが完了し、データが収集されます。 この記事では、結果で得られたすべての数値をダンプすることは意味がないと考えています。 ただし、 アーカイブとしてダウンロードできます 。 だから誰もが自分の目でそれらを見ることができます。

これらの結果が何であるかを経験的に示すことははるかに興味深いでしょう。 100,000ノードツリーのグラフの一部を見てみましょう。

以下はすべてカウントされ、秒単位で示されます。

図 1.ツリー全体をサンプリングする

次のグラフは、サンプリング関数の変動がツリーのさまざまな部分での検索に依存することを示しています。 実際、縦軸に沿った数字は、上記の手順を示しています。


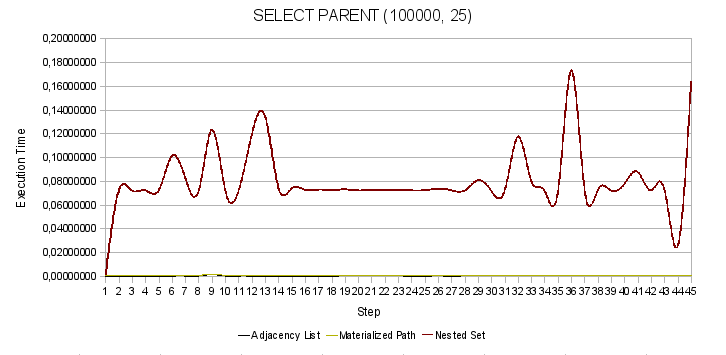図 2.親ノードを検索します


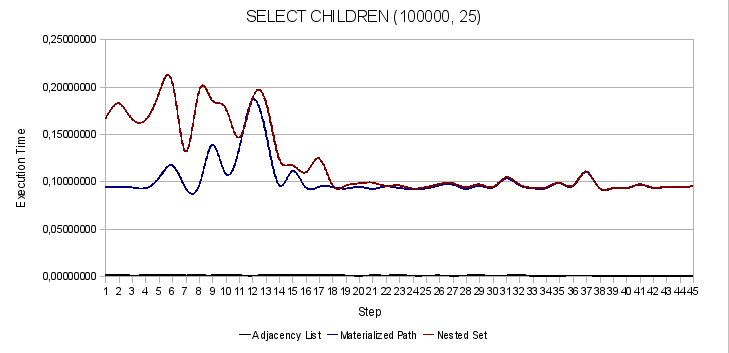図 3.特定のノードの相続人を検索する


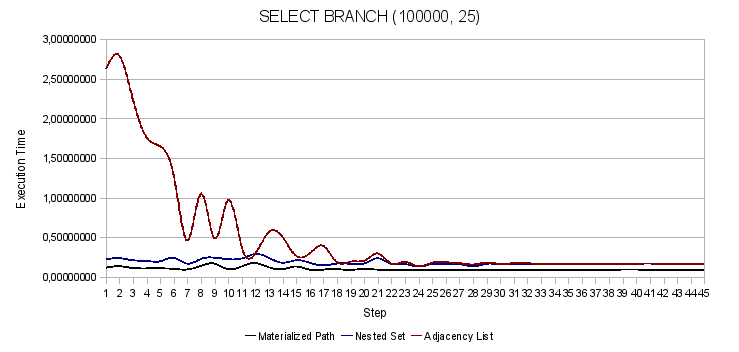図 4.特定のノードのブランチ全体を選択する


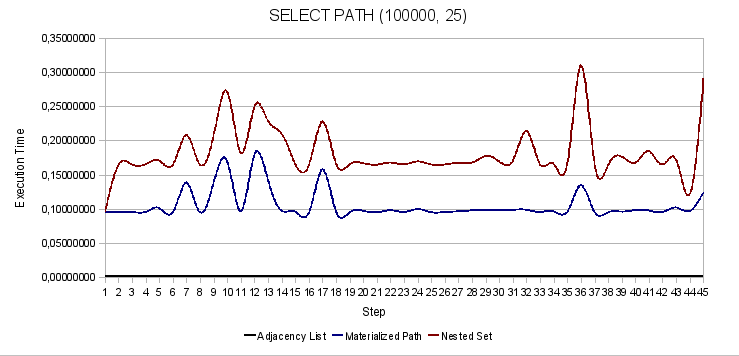図 5.ルートから特定のノードまでのフルパスを検索します

以下は、さまざまなタイプのツリーで実行された変更機能を示しています。


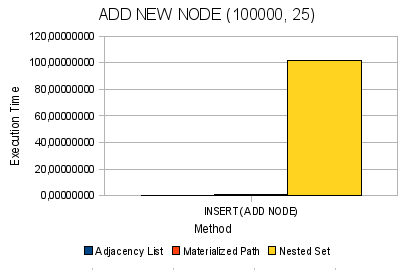図 6.ツリーに新しいノードを追加する


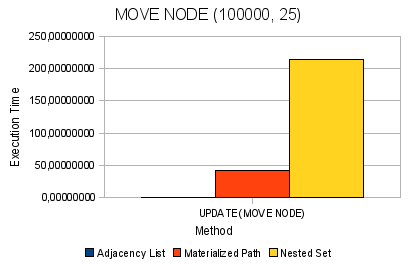図 7.ノードを移動する


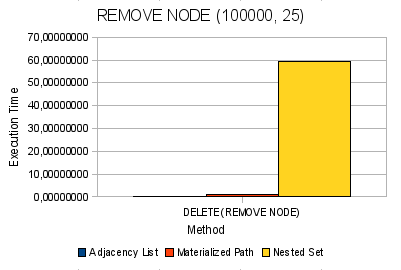図 8.ツリーからノードとそのすべての子孫を削除する

一般に、絶対的な用語では、次の結論を導き出すことができます。

隣接リスト：

結び目	すべて	パス	支店	親	子ども	追加	移動	削除する
100	0,00245	0.00016	0.00416	0.00009	0.00011	0,00059	0,00037	0.00009
1000	0,00335	0,00025	0,03579	0.00009	0.00011	0,00387	0,00037	0.00009
10,000	0.01244	0,00058	0.38146	0,00024	0,00036	0,03548	0,00081	0.00011
100,000	0.10798	0.00105	2,55379	0.00155	0,00138	0.06382	0.00119	0.13931
500,000	0.62305	0,00124	43,91373	0,00053	0,00209	0,05232	0,00077	0,00041

入れ子セット

結び目	すべて	パス	支店	親	子ども	追加	移動	削除する
100	0,00020	0.00015	0,00020	0.00017	0.00019	0.00367	0.02285	0.00314
1000	0.00129	0,00040	0,00093	0.00017	0,00059	0,02593	0.19237	0,02619
10,000	0.01387	0.00433	0.00825	0.01771	0.00460	0.38235	1,37070	0.37219
100,000	0.17165	0,07634	0.14261	0.17218	0,09953	101,749	213,461	59.1912
500,000	0,83033	0.41670	0.62517	0.42942	0.15318	1427.96	3,712.30	1627.97

マテリアライズドパス

結び目	すべて	パス	支店	親	子ども	追加	移動	削除する
100	0,00020	0.00017	0,00020	0.00016	0.00019	0,00076	0,02633	0,00059
1000	0,00137	0,00069	0,00107	0.00016	0,00071	0.00136	0.22232	0.00136
10,000	0.01560	0,00608	0.01372	0,00056	0,00737	0,00679	1,44434	0.00801
100,000	0.18680	0.10466	0.17608	0,00064	0.18546	0.92136	41.5875	1,06560
500,000	0.99102	0.56412	0.59418	0,00090	0.56800	2.02149	2950.40	1.67124

これらすべての数値とグラフについて考えてみましょう。

まず、少量のデータ（最大10,000ノードを含む）でのすべてのアルゴリズムは、すべての機能で非常に許容可能なパフォーマンスを示しました。

第二に、問題のある操作、すなわち：

ALツリーのブランチ全体をフェッチします。 この操作には最大2.5秒かかります。

テストで少しごまかしたことに注意してください。 そして、どうやって。 隣接リスト（AL）アルゴリズムでは、複数のテーブルを自分で結合する方法を使用してパス選択を実装しました。 はい、特に再帰的な方法でブランチをフェッチした結果と比較すると、結果は印象的です。 ただし、アプリケーションにこの関数を実装するこの方法を選択することはほとんどありません。 一時的な最適化でない限り。 結局、ネストの最大レベルを知る必要があり、1回のリクエストでの結合の数に関するDBMSの制限を下回らないようにする必要があります。 テストを行いました。

次に、ツリー内の10,000ノード（1秒以上）から始まるNSおよびMPアルゴリズムでのノード移動操作に問題があり、その後、すべてがさらに悪化します-MPの場合は100,000ノード-NSの場合、この数字は40秒を超えます- 4分 500,000ノードでは、数値は妥当な制限を完全に超えています。MPの場合はほぼ50分、NSの場合は1時間以上です。

NSの場合、残りの変更操作でも同様の状況が発生します。 10,000個の要素の場合、追加には1.5分以上かかり、500,000個の場合は23分以上かかります。 削除すると、同じ問題は100,000ノードではほぼ1分、500,000ノードでは27分以上になります。

MPは、ノードの削除および追加の操作において、非常に大きなボリュームでもかなり自信を持っています。 100,000個の要素を持つツリーでは、これらの操作は1秒以内に発生しますが、これは肯定的な結果以上のものです。 また、500,000ノードでも、これらの操作は数秒で発生します。

これは、ネストされたセットは、事実上静的なツリーで使用する必要があることを意味します。ツリーが変更された場合、それらは非常にまれです。 同時に、ALスキームをベースとして使用して、オンデマンドでツリーを完全に再構築するツールを作成することを検討する価値があります（任意のランダムツリーを生成するプログラムと同様）。 これは、事実から明らかなように、NS自体のルーチンよりもはるかに高速です。 または、マテリアライズドパスを優先してこのアルゴリズムを放棄します。

おわりに

判明したように、ネストされたセットやマテリアライズドパスなどのアルゴリズムの需要は、主に大量のデータによるものであり、アプリケーションにとって重要な検索および選択クエリを最適化できます。 または、クエリの最適化も重要な高負荷下で。 この場合、パスの検索や、隣接リストツリーのブランチ全体のフェッチなどの操作の最適化について話します。 実際には、近隣を検索する操作、ツリー全体または特定のノードのブランチで「葉」を選択する操作、およびここで考慮されていない他の操作（実際、SQLクエリのレベルではALにとって難しい）の最適化について話すことも価値があります。

得られた結果の背景に対して、ネストされたセットは、マテリアライズドパスより質的に劣っています。マテリアライズドパスは、削除と追加の操作に自信があります（そして、ツリー内のノードをどのくらいの頻度で移動しますか？）。 さらに、このアルゴリズムを最適化するための有望な見通しがあります。これについては、次の記事で説明します。

開発に頑張ってください！

_{これは私のブログのオリジナル記事のクロスポストです。}