すべての自然数の合計は、次の数列を使用して書くことができます
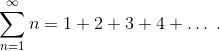
この無限級数の合計はいくらですか？ さらに読む前に、考えてみてください。 過去にこのようなシリーズに出会ったことがなく、数値シリーズ全体のトピックがあなたに近すぎない場合、この質問に対する答えはあなたにとって大きな驚きです。
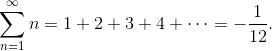
これは、一見、直感に完全に反する結果ですが、それでも厳密に証明できます。 しかし、証拠について話す前に、基本的な概念を無視して思い出す必要があります。
そもそも
、シリーズの「古典的な」
合計は、シリーズが存在し、有限である場合、その部分合計の制限です。 詳細は、ウィキペディアおよび関連文献に記載されています。 有限の限界が存在しない場合、シリーズは発散と呼ばれます。
たとえば、数値系列1 + 2 + 3 + 4 + ...の最初のkメンバーの部分和は、次のように記述されます。
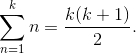
kが無限大になると、この合計が無限に増加することを理解するのは簡単です。 したがって、最初の系列は発散的であり、厳密に言えば、合計はありません。 ただし、最終値を発散系列に割り当てるには多くの方法があります。
行1 + 2 + 3 + 4 + ...は、分岐シリーズの唯一のものからはほど遠いです。 たとえば、
グランディシリーズ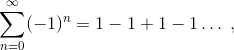
これも発散しますが
、Cesaroの加算方法を使用すると、このシリーズに最終値1/2を割り当てることができます。 Cesaroの合計は、一連の部分的な合計ではなく、その算術平均を使用した操作で構成されます。 自由なスタイルで推測できるように、Grandiシリーズの部分和は、シリーズのどのメンバーが合計の最後（+1または-1）であるかによって、0から1の間で振動するため、算術として値1/2になります。部分和の2つの可能な値の平均。
発散系列の別の興味深い例は、交互の系列
1-2 + 3-4 + ...で 、その部分和も振動します。 Abelの合計により、この行に最終値1/4を割り当てることができます。 アベル法は、ある意味ではチェザーロによる総和法の開発であるため、結果1/4は直感の観点から理解しやすいことに注意してください。
ここで重要なことは、加算方法は、数学者が発散系列に何らかの方法で対処するために思いついたトリックではないことです。 Cesaro加算またはAbel法を収束級数に適用する場合、これらの方法が与える答えは収束級数の古典的和に等しくなります。
ただし、Cesaro加算もAbelメソッドも、部分和の算術平均および算術平均の算術平均が発散するため、シリーズ1 + 2 + 3 + 4 + ...を使用できません。 さらに、値1/2または1/4が依然として何らかの方法で受け入れられ、対応するシリーズと関連付けられる場合、-1 / 12はシリーズ1 + 2 + 3 + 4 + ...と関連付けることが困難です。これは、正の無限シーケンスです。整数。
結果を-1/12にする方法はいくつかあります。 このメモでは、そのうちの1つ、つまり
ゼータ関数の正則化について簡単に説明します。 ゼータ関数を導入する
s = -1を代入すると、元の数値シリーズ1 + 2 + 3 + 4 + ...が得られます。 この関数では、いくつかの簡単な数学演算を実行します。
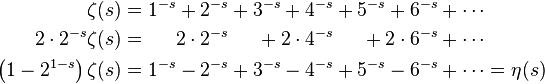
どこで
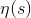ディリクレのイータ関数
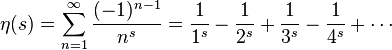s = -1の場合
、この関数は1-2 + 3-4 + 5-...の近くで既によく知られています。その「合計」は1/4です。 これで方程式を簡単に解くことができます
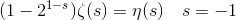
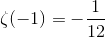
興味深いことに、この結果は物理学に応用されています。 たとえば、弦理論では。 Joseph Polchinskiの弦理論の22ページを参照してください。
一部の人々にとって、この理論の多くの結果の証拠が不足しているために、ストリング理論が説得力のある例ではない場合
、カシミール効果を計算しようとすると量子場理論に同様の方法が現れることにも言及でき
ます 。
2回歩かないように、ゼータ関数を使用したさらに興味深い
例が2つあります。
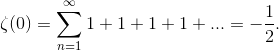
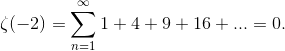
トピックに関する詳細情報を入手したい人のために、
Wikipediaの対応する記事を翻訳した後にこのメモを書くことにしました。リンクセクションでは、主に英語で多くの追加資料を見つけることができます。