エントリー
判明したように、アルゴリズム
のトピックはHabraコミュニティにとって興味深いものです。 したがって、約束したとおり、グラフの「古典的な」アルゴリズムの一連のレビューを開始します。
Habréの視聴者は異なり、トピックは多くの人にとって興味深いので、ゼロから始めなければなりません。 このパートでは、グラフとは何か、コンピュータ上でどのように表示されるか、なぜ使用されるのかを説明します。 このことをすでによく知っている人には事前に謝罪しますが、グラフでアルゴリズムを説明するには、まずグラフとは何かを説明する必要があります。 それなしでは仕方ありません。
基本
数学では、
グラフは多くのオブジェクトとそれらの間の接続の抽象的な表現です。 グラフはペア(V、E)で、Vは
頂点のセット、Eはペアのセットで、それぞれが接続です(これらのペアは
エッジと呼ばれ
ます )。
グラフは、
方向付けられている場合とされてい
ない場合があります。 有向グラフでは、接続は方向性があります(つまり、Eのペアが順序付けられます。たとえば、ペア(a、b)と(b、a)は2つの異なる接続です)。 同様に、無向グラフでは、接続は無方向です。したがって、接続(a、b)がある場合、接続(b、a)があることを意味します。
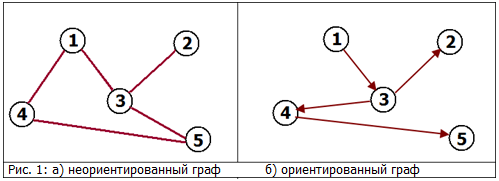 例:
例:無向カウント:近隣(生活中)。 (1)がネイバー(3)の場合、(3)はネイバー(1)です。 写真をご覧ください。 1.a
指向カウント:リンク。 サイト(1)はサイト(3)にリンクできますが、サイト(3)がサイト(1)にリンクしている必要はありません(可能ですが)。 写真をご覧ください。 1.b
頂点
の次数は、着信および発信することができます(無向グラフの場合、着信次数は発信と等しくなります)。
頂点vの入力次数は、フォーム(i、
v )のエッジの数、つまりvに「入る」エッジの数です。
頂点vの出力次数は、フォーム(
v 、i)のエッジの数、つまりvから「出る」エッジの数です。
これは完全に正式な定義(
発生率によるより正式な定義)ではありませんが、本質を完全に反映しています
グラフ内
のパスは、行の2つの頂点がエッジで接続されている頂点の有限シーケンスです。 パスは、グラフに応じて方向付けすることも方向付けないこともできます。 図1.aでは、パスは、たとえば、図1.b、[(1)、(3)、(4)、(5)]のシーケンス[(1)、(4)、(5)]です。
グラフにはまだ多くの異なるプロパティがありますが(たとえば、接続、双子葉、完全)、これらのプロパティすべてについては説明しませんが、以下の部分ではこれらの概念が必要になります。
グラフ表示
グラフを隣接リストおよび隣接行列として表すには、2つの方法があります。 どちらの方法も、指向グラフと非指向グラフの表現に適しています。
隣接行列この方法は、エッジの数(| E |)が2乗した頂点の数(| V |
2 )にほぼ等しい
密なグラフを表すのに便利です。
このビューでは、サイズ| V |の行列を埋めます。 x | V | 次のように:
A [i] [j] = 1(iからjへのエッジがある場合)
A [i] [j] = 0(それ以外の場合)
この方法は、有向グラフと無向グラフに適しています。 無向グラフの場合、行列Aは対称です(つまり、A [i] [j] == A [j] [i]。iとjの間にエッジがある場合、iからjのエッジでもあるため、 jからiへのエッジ)。 このプロパティのおかげで、要素をマトリックスの上部、メインの対角線上にのみ保存することで、メモリの使用をほぼ半減できます)
この表示方法では、セルA [v] [u]を調べるだけで、頂点vとuの間にエッジがあるかどうかをすばやく確認できることは明らかです。
一方、この方法は行列を格納するためにO(| V |
2 )メモリを必要とするため、非常に面倒です。
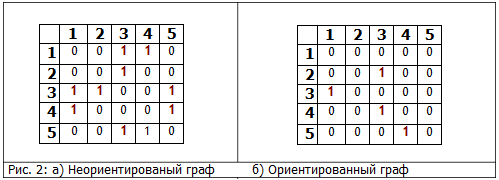
図 図2のグラフの2つの表現 1隣接行列を使用。
隣接リストこの表示方法は、スパースグラフ、つまりエッジの数が正方形の頂点の数よりはるかに少ないグラフ(| E | << | V |
2 )により適しています。
このビューは、| V |を含むAdj配列を使用します。 リスト。 各リストAdj [v]にはuのすべての頂点が含まれているため、vとuの間にエッジがあります。 プレゼンテーションに必要なメモリはO(| E | + | V |)です。これは、スパースグラフの隣接行列よりも優れた指標です。
この表示方法の主な欠点は、エッジ(u、v)が存在するかどうかをすばやく確認する方法がないことです。
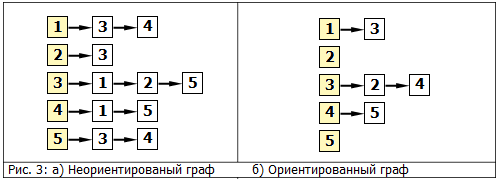
図 図3は、図のグラフの表現を示しています。 1隣接リストを使用。
申込み
この場所を読んだ人はおそらく自分自身に質問をしましたが、グラフはどこで使用できますか。 私が約束したように、例を挙げようとします。 最初に思い浮かぶのは、ソーシャルネットワークです。 グラフの頂点は人であり、関係の端(友情)です。 グラフは見当違いになる可能性があります。つまり、私は友達である人としか友達になれません。 または指向(LJなど)。ここでは、人を追加することなく、人を友人として追加できます。 彼があなたを追加すると、あなたは「相互の友人」になります。 つまり、2つのrib骨があります:(彼、あなた)と(あなた、彼)
すでに述べたグラフの別のアプリケーションは、サイトからサイトへのリンクです。 検索エンジンを作成し、サイトBにリンクしているサイトの数、サイトAにリンクしているサイトの数を考慮しながら、どのサイトにさらにリンクがあるか(サイトAなど)を考慮したいとします。これらのリンクの隣接行列があります。 このマトリックスで何らかの計算を行う何らかの評価計算システムを導入する必要があります。それから...それはGoogle(より正確には、PageRank)=)です。
おわりに
これは、次の部分に必要な理論の小さな部分です。 私はあなたがそれを理解し、そして最も重要なこととしてそれを気に入って、さらなる部分を読むことに興味があることを望みます! コメントにフィードバックや提案を残してください。
次の部分で
BFS-幅検索アルゴリズム
書誌
Kormen、Lizerson、Riverst、Stein-アルゴリズム。 構築と分析。 ウィリアムズ出版社、2007。
グラフ理論用語集アール-ウィキペディアの記事この記事は私のブログからのクロスポストです-「
そのままのプログラミング-プログラマーのメモ」
______________________