プロローグ
週末に発行された記事の続きで
。コンパイラは、おそらくシステムプログラミングで最も興味深いトピックの1つです。
この記事では、理想的なコンパイラー、または少なくとも機能するコンパイラーの作成方法については説明しませんが、トポロジーネットワークソートの方法を使用して、作業のいくつかの側面を明確にするのに役立ちます。
ネットワークとは何ですか?
ネットワークは非輪郭指向のグラフです(前の記事では、輪郭の問題とそれらを見つける方法が扱われていました)。
アルゴリズムには、いくつかのプロパティが必要です。それらのいくつかについては、最初の記事で詳しく説明しました。

写真からわかるように、各頂点は、そこに進入するアークの数(
アプローチの半度 )、およびそこから他の頂点に発するアークの数(
結果の半度 )によって特徴付けられます。
頂点に
入力アークがない場合、その頂点はネットワークの
ソースと呼ばれます。
頂点に
出力アークがない場合、その頂点はネットワークの
ドレインと呼ばれます。

アプリケーションアセンブリの例でネットワークを考えてみましょう。
ファイルは頂点で示されます。
ネットワークでのアークの役割は、図から理解しやすいです。
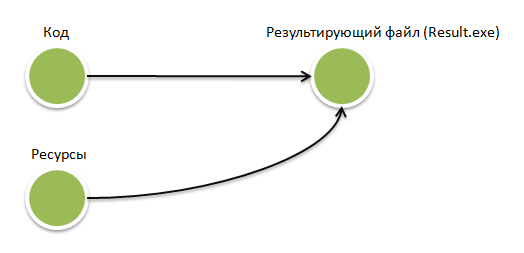
「コード」の上部から「結果ファイル」の上部に行く弧は、Result.exeを受信する前に「コード」を処理する必要があることを示します
頂点を処理する前に、その頂点を参照するすべての頂点を処理する必要があります。
小さな描かれたネットワークを見ると、すべてが単純に見えます。
現実に近づき、小さなプログラムの構築を検討しましょう。
例1:
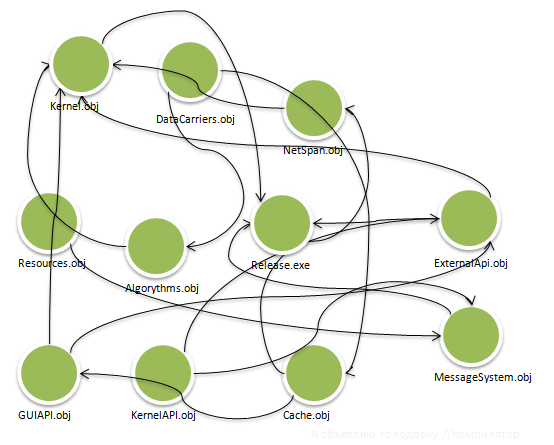
残念ながら、最新のコンパイラでさえ、ここで正しいビルドシーケンスを見るのにそれほど目が離せません。
アルゴリズム
コンパイラーは、最初に何をすべきか、次に何をすべきかをどのように理解していますか?
まず、アルゴリズムに必要なものを記述し、次にコードを提供します。
したがって、私たちの目標は、いくつかのレベルで構成されるネットワークを作成することです。

図から、1つのレベル内のタスクは下位レベルのタスクのみに依存し、互いに独立していることがわかります。
この場合、目標を達成するには、最初にレベル0のすべてのタスクを任意の順序で完了し、次に任意の順序でレベル1のタスクなどをレベル3(最後)に完了する必要があります。
この問題を解決するには、グラフを行列の形で表す必要があります(頂点iから頂点jに弧がある場合はij要素= 1、弧がない場合は0です)。
もう1つの例を考えてみましょう。
例2:

表の下の行には、すべての頂点に対するアプローチの準度合いが示されています。 各数値は、マトリックスの対応する列の単位の合計を反映しています。
アルゴリズムの最初のステップでは、半次のエントリがゼロのすべての頂点を選択し、ゼロレベルに入れて、精神的にグラフから除外します。
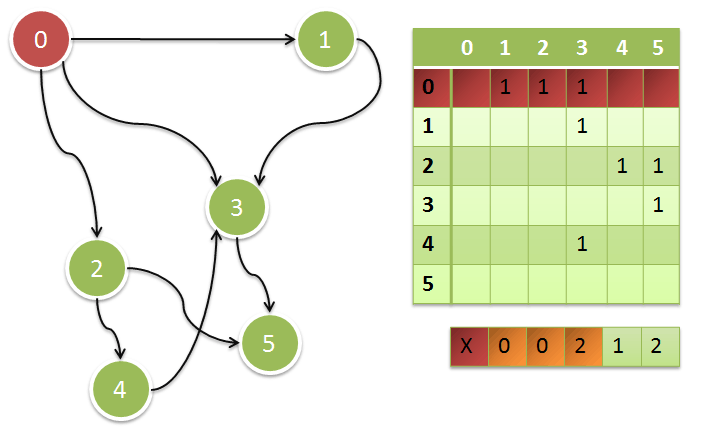
その結果、(処理された頂点に対応する行列の行を考慮しなくなりました)、残りの頂点の半次のエントリは減少します。
次に、アプローチのセミディグリーがゼロである
残りの頂点で同じことを行い、それらを最初のレベルに入れます

次の手順も同様に実行されます。
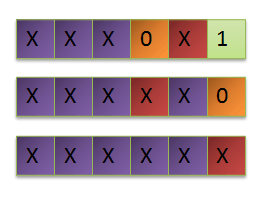
最初は、グラフが等高線でないことを要求しました。この要件のおかげで、各ステップで、アプローチの準度がゼロの新しい頂点ができます。
例1からネットワークにアルゴリズムを適用します。

実装例
必要な基本フレームワーク:
public class GraphNode
{
public List <GraphNode> LinkedNodes;
}
public class Graph
{
public List <GraphNode> nodes;
public void TopologicSort( out List < string > algResult, bool animated)
}
* This source code was highlighted with Source Code Highlighter .
すべてのネットワークノードの呼び出しの準度の配列を返す補助関数。
int ?[] GetInputNodesArray()
{
int ?[] array = new int ?[ this .nodes.Count];
for ( int i = 0; i < this .nodes.Count; i++)
{
array[i] = this .nodes[i].LinkedDownNodes.Count;
}
return array;
}
* This source code was highlighted with Source Code Highlighter .
そして最後に、アルゴリズム:
public void TopologicSort()
{
List < List <GraphNode>> levels = new List < List <GraphNode>>();
int ?[] workArray = GetInputNodesArray();
int completedCounter = 0;
int currentLevel = 0;
bool pathFound;
while (completedCounter != this .nodes.Count)
{
levels.Add( new List <GraphNode>());
// ,
// , ,
// .
for ( int i = 0; i < this .nodes.Count; i++)
{
if (workArray[i] == 0)
{
workArray[i] = null ;
}
}
for ( int i = 0; i < this .nodes.Count; i++)
{
if (workArray[i] == null )
{
// ,
//
//
levels[currentLevel].Add( this .nodes[i]);
this .nodes[i].Tag = currentLevel; //
foreach (GraphNode node in this .nodes[i].LinkedNodes)
{
int linkedNode = this .nodes.IndexOf(node);
workArray[linkedNode]--;
}
workArray[i] = -1; //
completedCounter++;
}
}
currentLevel++;
}
}
* This source code was highlighted with Source Code Highlighter .
エピローグ
コンパイラはこのアルゴリズムの使用に限定されず、たとえばニューラルネットワークのプログラミングや大規模プロジェクトの計画などにも使用できます。
次回は、グラフ上の最短パスを見つけるためのアルゴリズム(ダイクストラのアルゴリズムとウェーブフロントアルゴリズム)についての話があります。
ソースコード
C#のプログラムとソース:
ダウンロードこのリンクには、はるかに機能的なプログラムと、ソート用のネットワークのいくつかの例があります。
アルゴリズムのステップを省略したプレゼンテーション:
ダウンロード